中心对称图形都可以过对称中心作一条直线把它分成面积相等的两部分.例如:经过圆心的直线把圆分成两个面积相等的两部分.请你各画一条直线将下面的两个图形分成面积相等的两部分.
商场某种商品平均每天可销售30件,每件盈利50元. 为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.设每件商品降价x元. 据此规律,请回答:
(1)商场日销售量增加 ▲件,每件商品盈利 ▲元(用含x的代数式表示);
(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元?
某花圃用花盆培育某种花苗,经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时,平均单株盈利3圆;以同样的栽培条件,若每盆每增加1株,平均单株盈利就减少0.5元.要使每盆的盈利达到10元,每盆应该植多少株?(要求两种解法)
(2011安徽芜湖,20,8分) 如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为(
如图,用两段等长的铁丝恰好可以分别围成一个正五边形和一个正六边形,其中正五边形的边长为( )cm,正六边形的边长为(
)cm,正六边形的边长为(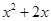 )cm
)cm .求这两段铁丝的总长.
.求这两段铁丝的总长. 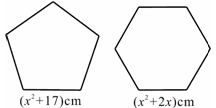
如图,邻边不等的矩形花圃ABCD,它的一边AD利用已有的围墙,另外三边所围的栅栏的总长度是6m.若矩形的面积为4m2,则AB的长度是 ▲ m(可利用的围墙长度超过6m).
随着经济的发展,尹进所在的公司每年都在元月一次性的提高员工当年的月工资.尹进2008 年的月工资为2000 元,在2010 年时他的月工资增加到2420 元,他2011年的月工资按2008 到2010 年的月工资的平均增长率继续增长.
(1)尹进2011年的月工资为多少?
(2)尹进看了甲、乙两种工具书的单价,认为用自己2011年6 月份的月工资刚好购买若干本甲种工具书和一些乙种工具书,当他拿着选定的这些工具书去付书款时,发现自己计算书款时把这两种工具书的单价弄对换了,故实际付款比2o11年6月份的月工资少了242 元,于是他用这242 元又购买了甲、乙两种工具书各一本,并把购买的这两种工具书全部捐献给西部山区的学校.请问,尹进总共捐献了多少本工具书?