(本题12分)已知函数 在
在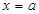 处取得极值.
处取得极值.
(1) 求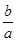 ;
;
(2 )设函数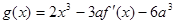 ,如果
,如果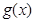 在开区间
在开区间 上存在极小值,求实数
上存在极小值,求实数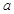 的取值范围.
的取值范围.
已知函数 (
( ),其中
),其中 .
.
(1)当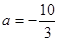 时,讨论函数
时,讨论函数 的单调性;
的单调性;
(2)若函数 仅在
仅在 处有极值,求
处有极值,求 的取值范围;
的取值范围;
(3)若对于任意的 ,不等式
,不等式 在
在 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
已知椭圆 :
:
 的左、右焦点分别为
的左、右焦点分别为 离心率
离心率
 ,点
,点 在且椭圆E上,
在且椭圆E上,
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设过点 且不与坐标轴垂直的直线交椭圆
且不与坐标轴垂直的直线交椭圆 于
于 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴交于点
轴交于点 ,求点
,求点 横坐标的取值范围.
横坐标的取值范围.
(Ⅲ)试用 表示
表示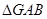 的面积,并求
的面积,并求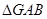 面积的最大值
面积的最大值
如图,已知 平面
平面 ,
, 平面
平面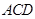 ,△
,△ 为等边三角形,
为等边三角形,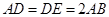 ,
,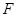 为
为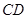 的中点.
的中点.
(1) 求证: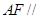 平面
平面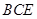 ;
;
(2) 求证:平面 平面
平面 ;
;
(3) 求直线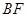 和平面
和平面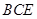 所成角的正弦值.
所成角的正弦值.
甲、乙、丙三人分别独立的进行某项技能测试,已知甲能通过测试的概率是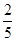 ,甲、乙、丙三人都能通过测试的概率是
,甲、乙、丙三人都能通过测试的概率是 ,甲、乙、丙三人都不能通过测试的概率是
,甲、乙、丙三人都不能通过测试的概率是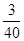 ,且乙通过测试的概率比丙大.
,且乙通过测试的概率比丙大.
(Ⅰ)求乙、丙两人各自通过测试的概率分别是多少;
(Ⅱ)求测试结束后通过的人数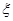 的数学期望
的数学期望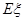 .
.
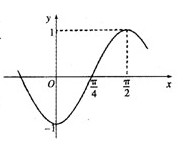
已知函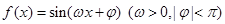 的部分图象如图所示:
的部分图象如图所示:
(1)求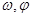 的值;
的值;
(2)设 ,当
,当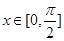 时,求函数
时,求函数 的值域.
的值域.