已知函数 (
( 且
且 )
)
(1)若函数 在
在 上的最大值与最小值的和为2,求
上的最大值与最小值的和为2,求 的值;
的值;
(2)将函数 图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,得到函数
图象上所有的点向左平移2个单位长度,再向下平移1个单位长度,得到函数 的图象,写函数
的图象,写函数 的解析式;
的解析式;
(3)若(2)中平移后所得的函数 的图象不经过第二象限,求
的图象不经过第二象限,求 的取值范围.
的取值范围.
设函数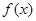 =
=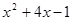 .
.
(1)若对一切实数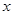 ,
,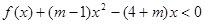 恒成立,求m的取值范围;
恒成立,求m的取值范围;
(2)若对于任意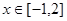 ,
,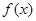
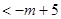 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知函数 ,
,
(1)当 时,解不等式
时,解不等式 ;
;
(2)比较 的大小;
的大小;
(3)解关于x的不等式 .
.
已知向量 ,其中
,其中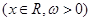 ,函数
,函数 的最小正周期为
的最小正周期为 ,最大值为3.
,最大值为3.
(1)求 和常数
和常数 的值;
的值;
(2)求当 时,函数
时,函数 的值域.
的值域.
已知数列{ }为等差数列,且
}为等差数列,且 =-6,
=-6, =0.
=0.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若等比数列{ }满足
}满足 =-8,
=-8, ,求数列{
,求数列{ }的前n项和
}的前n项和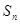 .
.
设数列 的前
的前 项和为
项和为 .若对任意的正整数
.若对任意的正整数 ,总存在正整数
,总存在正整数 ,使得
,使得 ,则称
,则称 是“
是“ 数列”.
数列”.
(1)若数列 的前
的前 项和为
项和为 ,证明:数列
,证明:数列 是“
是“ 数列”;
数列”;
(2)设 是等差数列,其首项
是等差数列,其首项 ,公差
,公差 ,若
,若 是“
是“ 数列”,求
数列”,求 的值;
的值;
(3)证明:对任意的等差数列 ,总存在两个“
,总存在两个“ 数列”
数列” 和
和 ,使得
,使得
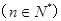 成立.
成立.