设数列
的前
项和为
．若对任意的正整数，总存在正整数
，使得
，则称是“
数列”．
（1）若数列的前项和为
，证明：数列是“数列”；
（2）设是等差数列，其首项
，公差
，若是“数列”，求
的值；
（3）证明：对任意的等差数列，总存在两个“数列”
和
，使得
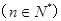成立．
1弧度的圆心角所对的弦长为2，求这个圆心角所对的弧长及圆心角所夹的扇形的面积．
（1）一个半径为r的扇形，若它的周长等于弧所在的半圆的长，那么扇形的圆心角是多少弧度？是多少度？扇形的面积是多少？
（2）一扇形的周长为20 cm，当扇形的圆心角α等于多少弧度时，这个扇形的面积最大？
在单位圆中画出适合下列条件的角α的终边的范围，并由此写出角α的集合：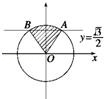
（1）sin α≥
；
（2）cos α≤﹣
．
已知角α的终边在直线3x+4y=0上，求sinα，cosα，tanα的值．
（本小题满分16分）已知椭圆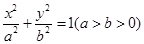
的两个焦点分别为
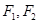，A为上端点，P为椭圆上任一点（与左、右顶点不重合）.
（1）若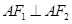
，求椭圆的离心率；
（2）若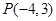
且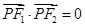
，求椭圆方程；
（3）若存在一点P使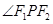
为钝角，求椭圆离心率的取值范围.