在单位圆中画出适合下列条件的角α的终边的范围,并由此写出角α的集合: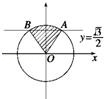
(1)sin α≥ ;
;
(2)cos α≤﹣ .
.
(本小题满分12分)如图4,四棱锥P—ABCD中,底面ABCD是直角梯形,AB//CD,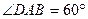 ,AB=AD=2CD,侧面
,AB=AD=2CD,侧面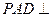 底面ABCD,且
底面ABCD,且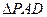 为等腰直角三角形,
为等腰直角三角形,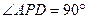 ,M为AP的中点。
,M为AP的中点。 (1)求证:
(1)求证:
(2)求证:DM//平面PCB;
(3)求平面PAD与平面PBC所成锐二面角的大小。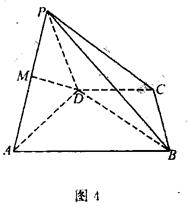
(本小题满分12分)已知向量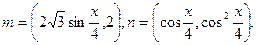
(1)若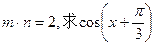 的值;
的值;
(2)记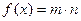 ,在
,在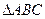 中,角A、B、C的对边分别是
中,角A、B、C的对边分别是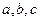 ,且满足
,且满足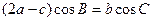 ,求
,求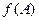 的取值范围。
的取值范围。
(本小题满分12分)某班50名学生在一模数学考试中,成绩都属于
区间[60,110]。将成绩按 如下方式分成五组:
如下方式分成五组:
第一组[60,70);第二组[70,80);第三组[80,90); 第四组[90,100);第五组[100,110]。
第四组[90,100);第五组[100,110]。
部分频率分布直方图如图3所示,及格(成绩不小于90分)的人数为20。
(1)请补全频率分布直方图;
(2)在成绩属于[70,80)∪[90,100]的学生中任 取
取
两人,成绩记为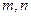 ,求
,求 的概率;
的概率;
(3)在该班级中任取4人,其中及极格人数记为随机变
量X,写出X的分布列(结 果只要求用组合数
果只要求用组合数
表示),并求出期望E(X)。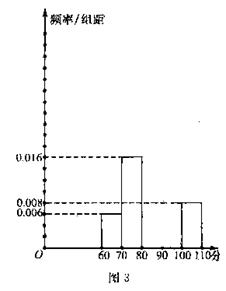
在数列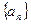 中,
中,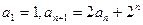
(1)设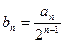 ,证明:数列
,证明:数列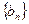 是等差数列
是等差数列
(2)求数列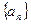 的前
的前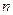 项和
项和
求 的值
的值