(1)计算:|- |+(-
|+(-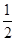 )-1-2sin45°+(
)-1-2sin45°+(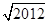 )0
)0
(2)先化简,再求值:(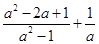 )÷
)÷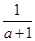 ,其中a=
,其中a= .
.
如图,对称轴为x=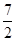 的抛物线经过点A(6,0)和B(0,4).
的抛物线经过点A(6,0)和B(0,4).
(1)求抛物线解析式;
(2)设点E(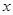 ,
,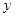 )是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与
)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与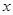 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量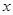 的取值范围;
的取值范围;
①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?
②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.
某农场要建一个长方形ABCD的养鸡场,鸡场的一边靠墙,(墙长25m)另外三边用木栏围成,木栏长40m。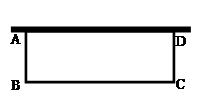
(1)若养鸡场面积为168m2,求鸡场的一边AB的长。
(2)请问应怎样围才能使养鸡场面积最大?最大的面积是多少?
(3)养鸡场面积能达到205m2吗?如果能,请给出设计方案,如果不能,请说明理由。
在一个不透明的口袋中有四个手感完全一致的小球,四个小球上分别标有数字-4,-1, 2, 5;
(1)从口袋中随机摸出一个小球,其上标明的数是奇数的概率是多少?
(2)从口袋中随机摸出一个小球不放回,再从中摸出第二个小球:
①请用表格或树状图表示先后摸出的两个小球所标数字组成的可能结果?
②求依次摸出的两个小球所标数字为横坐标,纵坐标的点位于第四象限的概率.
在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点.
(1)直接写出线段OB的长;
(2)将△OAB绕点O沿逆时针方向旋转90°得到△OA′B′。请你画出△OA′B′,并求在旋转过程中,点B所经过的路径弧BB′的长度.