如图,某公司入口处有一斜坡AB,坡角为12°,AB的长为3m,施工队准备将斜坡修成三级台阶,台阶高度均为hcm,深度均为30cm,设台阶的起点为C.
(1)求AC的长度;
(2)求每级台阶的高度h.
(参考数据:sin12°≈0.2079,cos12°≈0.9781,tan12°≈0.2126.结果都精确到0.1cm)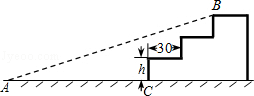
一个不透明的口袋中装有4个完全相同的小球,分别标有数字1、2、3、4,另有一个可以自由旋转的圆盘.被分成面积相等的3个扇形区,分别标有数字1、2、3(如图所示).小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一个人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于4,那么小颖去;否则小亮去.
(1)用树状图或列表法求出小颖参加比赛的概率;
(2)你认为该游戏公平吗?请说明理由;若不公平,请修改该游戏规则,使游戏公平.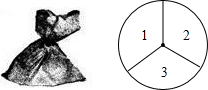
如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.
求证:OE=BC.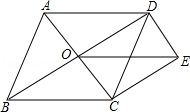
以下是根据全国人力资源和社会保障部公布的相关数据绘制的统计图的一部分,请你根据图中信息解答下列问题: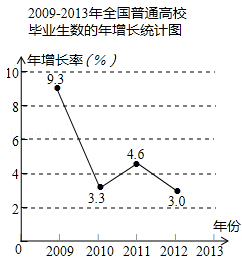
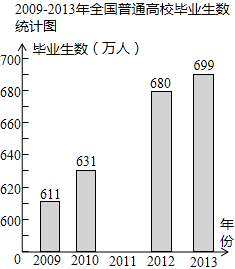
(1)求2013年全国普通高校毕业生数年增长率约是多少?(精确到0.1%)
(2)求2011年全国普通高校毕业生数约是多少万人?(精确到万位)
(3)补全折线统计图和条形统计图.
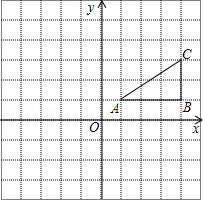
如图,方格纸中的每个小正方形边长都是1个长度单位,Rt△ABC的顶点均在格点上,建立平面直角坐标系后,点A的坐标为(1,1),点B的坐标为(4,1).
(1)先将Rt△ABC向左平移5个单位长度,再向下平移1个单位长度得到Rt△A1B1C1,试在图中画出Rt△A1B1C1,并写出点A1的坐标;
(2)再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2,试在图中画出Rt△A2B2C2,并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长.