(本小题满分14分)设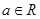 ,函数
,函数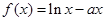 .
.
(1) 若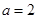 ,求曲线
,求曲线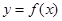 在
在 处的切线方程;
处的切线方程;
(2) 若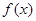 无零点,求实数
无零点,求实数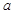 的取值范围;
的取值范围;
(3) 若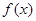 有两个相异零点
有两个相异零点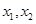 ,求证:
,求证: 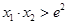 .
.
(本小题满分14分) 已知向量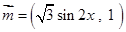 ,
, ,设函数
,设函数 .
.
(1)求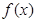 的单调递增区间;
的单调递增区间;
(2)在△ 中,
中, 、
、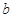 、
、 分别是角
分别是角 、
、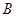 、
、 的对边,若
的对边,若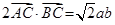 ,
, ,
, 求
求 .
.
(本小题满分12分)在数列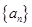 中,已知
中,已知
(1)求数列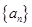 、
、 的通项公式;
的通项公式;
(2)设数列 满足
满足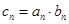 ,求
,求 的前n项和
的前n项和 .
.
(本小题满分12分)已知集合 ,
, .
.
(Ⅰ)求集合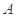 和
和 ;
;
(Ⅱ)若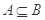 ,求实数
,求实数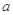 的取值范围.
的取值范围.
(本小题满分14分)设函数 R
R ,且
,且 为
为 的极值点.
的极值点.
(1)当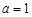 时,求
时,求 的单调递减区间;
的单调递减区间;
(2)若 恰有两解,试求实数
恰有两解,试求实数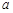 的取值范围;
的取值范围;
(3)在(1)的条件下,设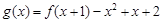 ,证明:
,证明: .
.
(本小题满分14分)已知函数 ,设曲线
,设曲线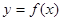 过点
过点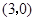 ,且在点
,且在点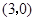 处的切线的斜率等于
处的切线的斜率等于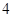 ,
,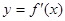 为
为 的导函数,满足
的导函数,满足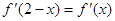 .
.
(1)求 ;
;
(2)设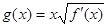 ,
,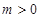 ,求函数
,求函数 在
在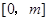 上的最大值;
上的最大值;
(3)设 ,若
,若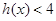 对
对 恒成立,求实数
恒成立,求实数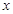 的取值范围.
的取值范围.