求使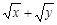 ≤
≤
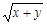 (x>0,y>0)恒成立的
(x>0,y>0)恒成立的 的最小值
的最小值
某市司法部门为了宣传《宪法》举办法律知识问答活动,随机对该市18~68岁的人群抽取一个容量为 的样本,并将样本数据分成五组:
的样本,并将样本数据分成五组: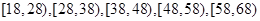 ,再将其按从左到右的顺序分别编号为第1组,第2组,
,再将其按从左到右的顺序分别编号为第1组,第2组,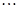 ,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.
,第5组,绘制了样本的频率分布直方图;并对回答问题情况进行统计后,结果如下表所示.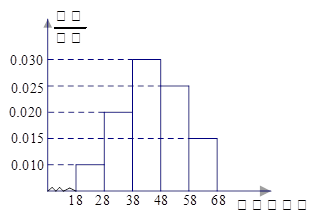
| 组号 |
分组 |
回答正确的人数 |
回答正确的人数占本组的比例 |
| 第1组 |
[18,28) |
5 |
0.5 |
| 第2组 |
[28,38) |
18 |
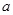 |
| 第3组 |
[38,48) |
27 |
0.9 |
| 第4组 |
[48,58) |
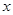 |
0.36 |
| 第5组 |
[58,68) |
3 |
0.2 |
(1)分别求出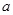 ,
,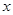 的值;
的值;
(2)从第2,3,4组回答正确的人中用分层抽样方法抽取6人,则第2,3,4组每组应各抽取多少人?
(3)在(2)的前提下,决定在所抽取的6人中随机抽取2人颁发幸运奖,求:所抽取的人中第2组至少有1人获得幸运奖的概率.
已知命题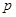 :实数
:实数 满足
满足 ;命题q:实数
;命题q:实数 满足
满足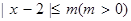 .
.
(1)当 时,若“
时,若“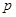 且
且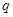 ”为真,求实数
”为真,求实数 的取值范围;
的取值范围;
(2)若“非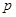 ”是“非
”是“非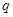 ”的必要不充分条件,求实数
”的必要不充分条件,求实数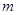 的取值范围.
的取值范围.
如图,斜三棱柱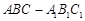 中,侧面
中,侧面 是菱形,
是菱形,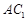 与
与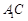 交于点
交于点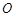 ,E是AB的中点.
,E是AB的中点.
求证:(1) 平面
平面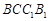 ;
;
(2)若 ,求证:
,求证: .
.
已知椭圆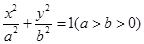 经过点
经过点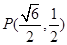 ,离心率为
,离心率为 ,动点M(2,t)(
,动点M(2,t)( ).
).
(1)求椭圆的标准方程;
(2)求以OM为直径且截直线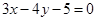 所得的弦长为2的圆的方程;
所得的弦长为2的圆的方程;
(3)设F是椭圆的右焦点,过点F作OM的垂线与以OM为直径的圆交于点N,证明线段ON的长为定值,并求出这个定值.
已知函数 ,且方程
,且方程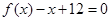 有两个实根
有两个实根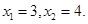
(1)求函数 的解析式;
的解析式;
(2)设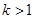 ,解关于
,解关于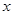 的不等式
的不等式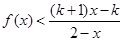 .
.