已知: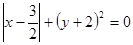 ,化简
,化简  再求值.
再求值.
吸烟有害健康!为配合“禁烟”行动,某校组织同学们在某社区开展了“你支持哪种戒烟方式”的问卷调查,征求市民的意见,并将调查结果整理后制成了如下统计图7,根据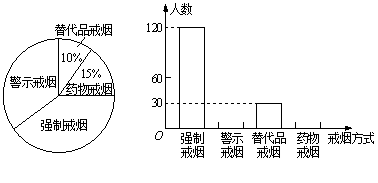
统计图解答:
(1)同学们一共随机调查了多少人?
(2)请你把两个统计图补充完整;
(3)假定该社区有1万人,请估计该地区大约有多少人支持“警示戒烟”这种方式。
如图,甲、乙两转盘都被分成3个面积相等的扇形.分别转甲盘、乙盘各一次(当转盘停下时指针指在边界线上时视为无效,重转)。(1)用树状图或列表法列举出转盘停下时两个指针所指区域内的数字之和的所有可能情况;(2)求转盘停下时两个指针所指区域内的数字之和为奇数的概率;(3)求转盘停下时两个指针所指区域内的数字之和大于6的概率。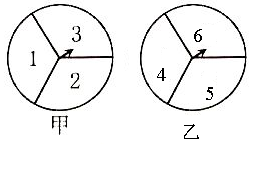
|
如图,AB是⊙O的直径,且AB=4,AC是弦,∠CAB=30°,求劣弧 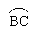 和弦AC的长.(弧长计算结果保留
和弦AC的长.(弧长计算结果保留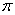 )
)

如图,已知等腰梯形ABCD,AD∥BC,∠D=120°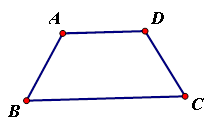
(1)用直尺和圆规作出∠BAD的平分线AE,交BC于点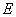 ,(保留作图痕迹,不要求写作法);
,(保留作图痕迹,不要求写作法);
(2)求证:四边形AECD是平行四边形。
 解不等式组
解不等式组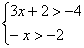 ,并将解集在数轴上表示出来。
,并将解集在数轴上表示出来。