如图，在平面直角坐标系xOy中，四边形ABCD是菱形，顶点A、C、D均在坐标轴上，且AB=5，sinB=
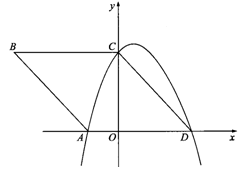
（1）求过A、C、D三点的抛物线的解析式；
（2）记直线AB的解析式为y1=mx+n，（1）中抛物线的解析式为y2=ax2+bx+c，求当y1＜y2时，自变量x的取值范围；
（3）设直线AB与（1）中抛物线的另一个交点为E，P点为抛物线上A、E两点之间的一个动点，当P点在何处时，△PAE的面积最大？并求出面积的最大值．
先化简再求值：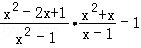
，其中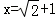
．
计算：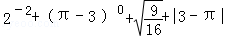
（结果保留π）
如图，一次函数y=x﹣5分别交x轴、y轴于A、B两点，二次函数y=﹣x2+bx+c的图象经过A、B两点．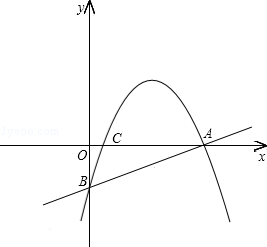
（1）求二次函数的解析式；
（2）设D、E是线段AB上异于A、B的两个动点（E点位于D点上方），DE=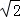
．
①若点D的横坐标为t，用含t的代数式表示D、E的坐标；
②抛物线上是否存在点F，使点F与点D关于x轴对称，如果存在，请求出△AEF的面积；如果不存在，请说明理由．
如图：已知△ABC中，AB=5，BC=3，AC=4，PQ∥AB，P点在AC上（与A、C不重合），Q在BC上．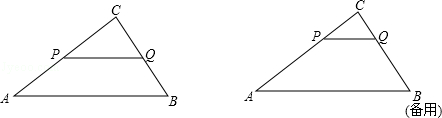
（1）当△PQC的面积与四边形PABQ的面积相等时，求CP的长；
（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长；
（3）试问：在AB上是否存在一点M，使得△PQM为等腰直角三角形？若不存在，请简要说明理由；若存在，请求出PQ的长．
如图，⊙C经过原点且与两坐标轴分别交于点A和点B，点A的坐标为（0，2），D为⊙C在第一象限内的一点且∠ODB=60°，解答下列各题：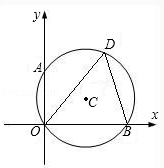
（1）求线段AB的长及⊙C的半径；
（2）求B点坐标及圆心C的坐标．