用分析法证明: .
.
(本题满分共14分)已知数列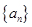 ,
,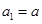 ,且
,且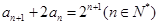 ,
,
(1)若 成等差数列,求实数
成等差数列,求实数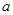 的值;(2)数列
的值;(2)数列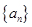 能为等比数列吗?若能,
能为等比数列吗?若能,
试写出它的充要条件并加以证明;若不能,请说明理由。
(本题满分共14分)已知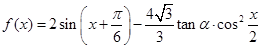 ,
,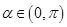 且
且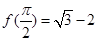 .
.
(1)求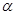 ;
;
(2)当 时,求函数
时,求函数 的值域.
的值域.
本题满分14分) 设函数f (x)=ln x+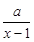 在(0,
在(0,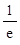 ) 内有极值.
) 内有极值.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若x1∈(0,1),x2∈(1,+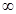 ).求证:f (x2)-f (x1)>e+2-
).求证:f (x2)-f (x1)>e+2-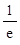 .
.
注:e是自然对数的底数.
(本题满分15分) 如图,椭圆C: x2+3y2=3b2(b>0).
(Ⅰ) 求椭圆C的离心率;
(Ⅱ) 若b=1,A,B是椭圆C上两点,且| AB | =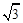 ,求△AOB面积的最大值.
,求△AOB面积的最大值.
(本题满分15分)四棱锥P-ABCD中,PA⊥平面ABCD,E为AD的中点,ABCE为菱形,∠BAD=120°,PA=AB,G,F分别是线段CE,PB上的动点,且满足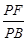 =
=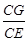 =λ∈(0,1).
=λ∈(0,1).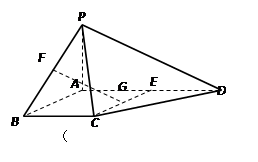
(Ⅰ) 求证:FG∥平面PDC;
(Ⅱ) 求λ的值,使得二面角F-CD-G的平面角的正切值为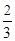 .
.