如图,在四棱锥  中,
中,  为等边三角形,平面
为等边三角形,平面  平面
平面 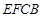 ,
,  ,
,  ,
, 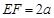 ,
,  ,
,  为
为  的中点.
的中点. 
(Ⅰ)求证:  ;
;
(Ⅱ)求二面角  的余弦值;
的余弦值;
(Ⅲ)若 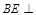 平面
平面  ,求
,求  的值.
的值.
【2015高考新课标1,理18】如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.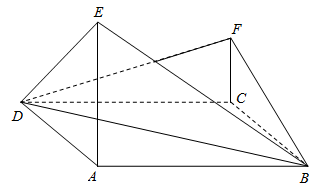
(Ⅰ)证明:平面AEC⊥平面AFC;
(Ⅱ)求直线AE与直线CF所成角的余弦值.
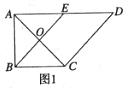
【2015高考陕西,理18】(本小题满分12分)如图 ,在直角梯形
,在直角梯形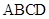 中,
中,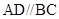 ,
,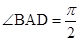 ,
,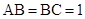 ,
, ,
,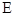 是
是 的中点,
的中点,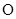 是
是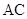 与
与 的交点.将
的交点.将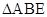 沿
沿 折起到
折起到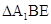 的位置,如图
的位置,如图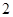 .
.
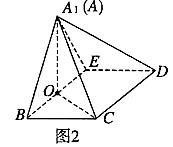
(Ⅰ)证明: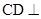 平面
平面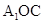 ;
;
(Ⅱ)若平面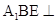 平面
平面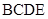 ,求平面
,求平面 与平面
与平面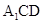 夹角的余弦值.
夹角的余弦值.
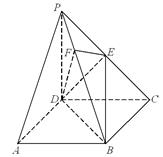
【2015高考湖北,理19】《九章算术》中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑.如图,在阳马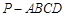 中,侧棱
中,侧棱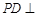 底面
底面 ,且
,且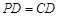 ,过棱
,过棱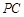 的中点
的中点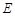 ,作
,作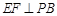 交
交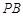 于点
于点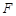 ,连接
,连接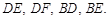
(Ⅰ)证明: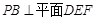 .试判断四面体
.试判断四面体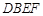 是否为鳖臑,若是,写出其每个面的直角(只需写
是否为鳖臑,若是,写出其每个面的直角(只需写
出结论);若不是,说明理由;
(Ⅱ)若面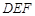 与面
与面 所成二面角的大小为
所成二面角的大小为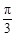 ,求
,求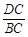 的值.
的值.
【2015高考四川,理18】一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设 的中点为
的中点为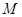 ,
, 的中点为
的中点为

(1)请将字母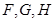 标记在正方体相应的顶点处(不需说明理由)
标记在正方体相应的顶点处(不需说明理由)
(2)证明:直线 平面
平面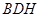
(3)求二面角 的余弦值.
的余弦值.