化简:
一次函数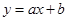 的图象与反比例函数
的图象与反比例函数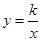 的图象交于A(1,4)、B(﹣2,m)两点,
的图象交于A(1,4)、B(﹣2,m)两点,
(1)求一次函数和反比例函数的关系式;
(2)画出草图,并根据草图直接写出不等式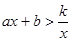 的解集.
的解集.
如图,在边长为1的正方形网格中有两个三角形△ABC和△DEF,试证这两个三角形相似.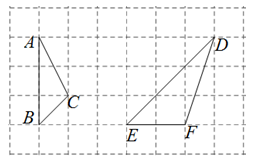
如图,在平面直角坐标系中,抛物线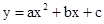 的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交
的顶点A的坐标为(3,15),且过点(-2,10),对称轴AB交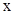 轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.
轴于点B,点E是线段AB上一动点,以EB为边在对称轴右侧作矩形EBCD,使得点D恰好落在抛物线上,点D′是点D关于直线EC的轴对称点.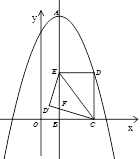
(1)求抛物线的解析式;
(2)若点D′恰好落在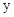 轴上的点(0,6)时,求此时D点的坐标;
轴上的点(0,6)时,求此时D点的坐标;
(3)直线CD′交对称轴AB于点F,
①当点D′在对称轴AB的左侧时,且△ED′F∽△CDE,求出DE:DC的值;
②连结B D′,是否存在点E,使△E D′B为等腰三角形?若存在,请直接写出BE:BC的值,若不存在请说明理由.
天猫商城旗舰店销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
,在销售过程中销售单价不低于成本价,而每件的利润不高于成本价的60%.
(1)设该旗舰店每月获得利润为w(元),求每月获得利润w(元)与销售单价x(元)之间的函数关系式,并确定自变量x的取值范围.
(2)当销售单价定为多少元时,每月可获得最大利润?每月的最大利润是多少?
(3)如果旗舰店想要每月获得的利润不低于2000元,那么每月的成本最少需要元?
(成本=进价×销售量)
如图,在△ABC中,AB=AC,以AB为直径的⊙O交AC与E,交BC与D.
(1)求证:D是BC的中点;
(2)求证:△BEC∽△ADC;
(3)若CE=5,BD=6.5,求AB的长.