如图,点E,F在BC上,BE=CF,∠A=∠D,∠B=∠C,AF与DE交于点O.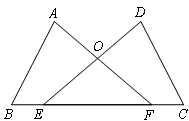
(1)求证:AB=DC;
(2)试判断△OEF的形状,并说明理由.
一艘船从A处以每小时36海里的速度向正东方向航行,且在A处测得岛C在其北偏东600方向,半小时后到B处测得该岛在其北偏东300方向,已知岛C方圆16海内的暗礁。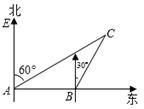
(1)试说明点B是否在暗礁区域;
(2)船继续东行有触礁危险吗?
已知:如图,Rt△ABC中,∠A=900。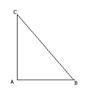
(1)求作:⊙O,使圆心在AC上,且与AB、BC相切;
(2)若∠B=600,AC= ,求⊙O的半径。
,求⊙O的半径。
先将下式化简,再选择一个你喜欢又使原式有意义的数代入求值。
为了求1+2+22+23+…+2100的值,可令S=1+2+22+23+…+2100,则2S=2+22+23+24+…+2101,因此2S﹣S=2101﹣1,所以S=2101﹣1,即1+2+22+23+…+2100=2101﹣1,仿照以上推理计算1+2+22+23+…+22014的值是
如图,在直角坐标系中,四边形OABC的OA,OC两边分别在x,y轴上,OA∥BC,BC=15cm,A点坐标为(16,0),C点坐标为(0,4).点P,Q分别从C,A同时出发,点P以2cm/s的速度由C向B运动,点Q以4cm/s的速度由A向O运动,当点Q到达点O时,点P也停止运动,设运动时间为t秒(0≤t≤4).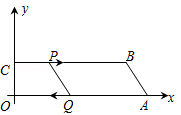
(1)求当t为多少时,四边形PQAB为平行四边形?
(2)求当t为多少时?PQ所在直线将四边形OABC分成左右两部分的面积比为1:2;
(3)直接写出在(2)的情况下,直线PQ的函数关系式.