如图1，已知△ABC中，AB＝BC＝1，∠ABC＝90°，把一块含30°角的△DEF的直角顶点D放在AC的中点上（直角三角板的短直角边为DE，长直角边为DF），将直角三角板DEF绕D点按逆时针方向旋转。
⑴在图1中，DE交AB于M，DF交BC于N。①说明DM＝DN；②在这一过程中，直角三角板DEF与△ABC的重叠部分为四边形DMBN，请说明四边形DMBN的面积是否发生变化？若发生变化，请说明是如何变化的？若不发生变化，求出其面积；
⑵继续旋转至如图2的位置，延长AB交DE于M，延长BC交DF于N，DM＝DN是否仍然成立？若成立，请给出理由；若不成立，请说明理由；
⑶继续旋转至如图3的位置，延长FD交BC于N，延长ED交AB于M，DM＝DN是否仍然成立？若成立，请给出结论，不用说明理由。
(1)解方程：① x2+4x－12="0" ② 3x2+5(2x+1)=0
(2)计算：
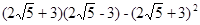
施工队要修建一个横断面为抛物线的公路隧道，其高度为6米，宽度OM为12米.现以O点为原点，OM所在直线为X轴建立直角坐标系（如图所示）.
（1）直接写出点M及抛物线顶点P的坐标；
（2）求出这条抛物线的函数解析式；
（3）施工队计划在隧道门口搭建一个矩形“脚手架”CDAB，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下.
(12分)如图，已知抛物线
与x轴的一个交点为A(-1,0)，与y轴的正半轴交于点C．
⑴直接写出抛物线的对称轴，及抛物线与x轴的另一个交点B的坐标；
⑵当点C在以AB为直径的⊙P上时，求抛物线的解析式；
已知一次函数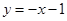
与反比例函数
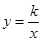的图象都过点A（
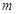，1）。（1）求
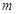的值，并求反比例函数的解析式；（2）求正比例函数与反比例函数的另一个交点B的坐标；
（3）求△AOB的面积。
上海世博会期间，某商店出售一种海宝毛绒玩具，每件获利60元，一天可售出20件，经市场调查发现每降价1元可多售出2件，设降价x元，商店每天获利y 元。⑴求y与x 的函数关系式。
⑵当降价多少元时，商店可获最大利润？最大利润是多少？