(本题13分) “你低碳了吗?”这是某市为倡导建设节约型社会而发布的公益广告里的一句话.活动组织者为了了解这则广告的宣传效果,随机抽取了120名年龄在[10,20) ,[20,30) ,…, [50,60) 的市民进行问卷调查,由此得到的样本的频率分布直方图如图所示.
(1) 根据直方图填写右面频率分布统计表;
(2) 根据直方图,试估计受访市民年龄的中位数(保留整数);
(3) 按分层抽样的方法在受访市民中抽取 名市民作为本次活动的获奖者,若在[10,20)的年龄组中随机抽取了6人,则
名市民作为本次活动的获奖者,若在[10,20)的年龄组中随机抽取了6人,则 的值为多少?
的值为多少?
已知平行四边形ABCD和矩形ACEF所在的平面互相垂直,AB=1,AD=2,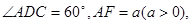 (I)求证:AC⊥BF;
(I)求证:AC⊥BF;
(II)若二面角F—BD—A的大小为60°,求a的值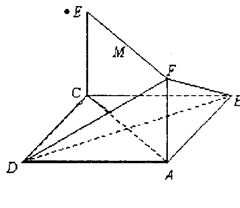
已知 为实数,
为实数, (1)求导数
(1)求导数 ;(2)若
;(2)若 ,求
,求 在
在 上的最大值和最小值
上的最大值和最小值
(本小题满分14分)
已知 其中e是自然对数的底数,
其中e是自然对数的底数,
(1)讨论a=1时, 的单调性、极值;
的单调性、极值;
(2)是否存在实数a,使 的最小值是3,若存在,求出a的值;若不存在,说明理由;
的最小值是3,若存在,求出a的值;若不存在,说明理由;
(3)求证:在(1)的条件下,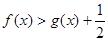 。
。
(本小题满分12分)
已知椭圆 :
: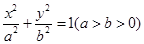 的离心率为
的离心率为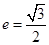 ,且过点
,且过点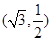 .
.
(Ⅰ)求椭圆 的标准方程;
的标准方程;
(Ⅱ)垂直于坐标轴的直线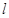 与椭圆
与椭圆 相交于
相交于 、
、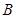 两点,若以
两点,若以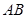 为直径的圆
为直径的圆 经过坐标原点.证明:圆
经过坐标原点.证明:圆 的半径为定值.
的半径为定值.
(本小题满分12分)
如图,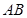 为圆
为圆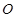 的直径,点
的直径,点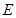 、
、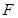 在圆
在圆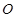 上,
上,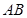 ∥
∥ ,矩形
,矩形 所在的平面和圆
所在的平面和圆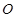 所在的平面互相垂直,且
所在的平面互相垂直,且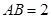 ,
, .
.
(1)求证: 平面
平面 ;
;
(2)设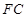 的中点为
的中点为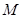 ,求证:
,求证: ∥平面
∥平面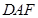 ;
;
(3)求三棱锥 的体积.
的体积.