已知二次函数f(x)=ax2+bx+1(a>0),F(x)=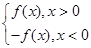 若f(-1)=0,且对任意实数x均有f(x)≥0成立.
若f(-1)=0,且对任意实数x均有f(x)≥0成立.
(1)求F(x)的表达式;
(2)当x∈[-2,2]时,g(x)=f(x)-kx是单调函数,求k的取值范围.
已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)的图象上任意一点P关于原点对称的点Q的轨迹恰好是函数f(x)的图象.
(1)写出函数g(x)的解析式;
(2)当x∈[0,1)时总有f(x)+g(x)≥m成立,求m的取值范围.
如图,四棱锥P-ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点.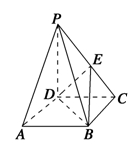
(1)证明:PA∥平面BDE;
(2)求二面角B-DE-C的余弦值.
已知函数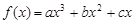 的导函数为
的导函数为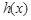 ,
,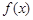 的图象在点
的图象在点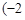 ,
,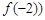 处的切线方程为
处的切线方程为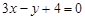 ,且
,且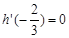 ,直线
,直线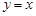 是函数
是函数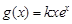 的图象的一条切线.
的图象的一条切线.
(1)求函数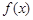 的解析式及
的解析式及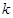 的值;
的值;
(2)若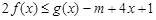 对于任意
对于任意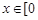 ,
,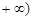 恒成立,求实数
恒成立,求实数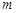 的取值范围.
的取值范围.
如图,焦距为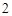 的椭圆
的椭圆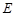 的两个顶点分别为
的两个顶点分别为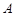 和
和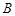 ,且
,且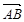 与n
与n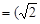 ,
,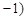 共线.
共线.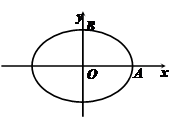
(1)求椭圆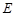 的标准方程;
的标准方程;
(2)若直线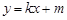 与椭圆
与椭圆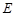 有两个不同的交点
有两个不同的交点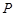 和
和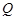 ,且原点
,且原点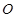 总在以
总在以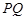 为直径的圆的内部,
为直径的圆的内部,
求实数 的取值范围.
的取值范围.