阅读材料:
小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如3+2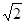 =(1+
=(1+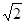 )
)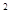 ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设a+b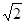 =(m+n
=(m+n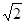 )
)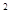 (其中a、b、m、n均为正整数),则有a+b
(其中a、b、m、n均为正整数),则有a+b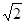 =m2+2n2+2mn
=m2+2n2+2mn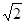 ,
,
∴a= m2+2n2,b=2mn.这样小明就找到了一种把部分a+b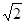 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
(1)当a、b、m、n均为正整数时,若a+b =(m+n
=(m+n )
)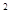 ,用含m、n的式子分别表示a、b,得:a= , b= ;
,用含m、n的式子分别表示a、b,得:a= , b= ;
(2)利用所探索的结论,找一组正整数a、b、m、n填空:
+  =( +
=( +  )
)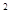 ;
;
(3)若a+4 =(m+n
=(m+n )
)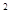 ,且a、m、n均为正整数,求a的值.
,且a、m、n均为正整数,求a的值.
(1)计算:3(–π)0– + (–1)2011
(2)先化简,再求值: – ,其中x = –3
(3)如图,平行四边形ABCD的对角线AC、BD交于点O,E、F在AC上,G、H在BD上,且AF=CE,BH=DG,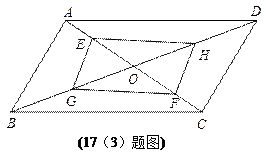 求证:AG∥HE
求证:AG∥HE
已知抛物线的顶点是C (0,a) (a>0,a为常数),并经过点(2a,2a),点D(0,2a)为一定点.
(1)求含有常数a的抛物线的解析式;
(2)设点P是抛物线任意一点,过P作PH⊥x轴,垂足是H,求证:PD = PH;
(3)设过原点O的直线l与抛物线在第一象限相交于A、B两点,若DA=2DB,且S△ABD = 4,求a的值.
 |
已知:在△ABC中,以AC边为直径的⊙O交BC于点D,在劣弧上取一点E使∠EBC = ∠DEC,延长BE依次交AC于G,交⊙O于H.
(1)求证:AC⊥BH
(2)若∠ABC= 45°,⊙O的直径等于10,BD =8,求CE的长.
 |
如图,飞机沿水平方向(A、B两点所在直线)飞行,前方有一座高山,为了避免飞机飞行过低,就必须测量山顶M到飞行路线AB的距离MN.飞机能够测量的数据有俯角和飞行的距离(因安全因素,飞机不能飞到山顶的正上方N处才测飞行距离),请设计一个距离MN的方案,要求:
(1)指出需要测量的数据(用字母表示,并在图中标出);
(2)用测出的数据写出求距离MN的步骤.
 |
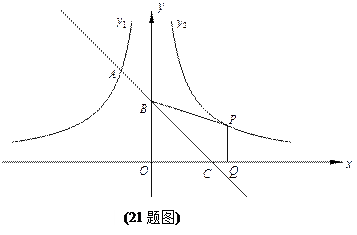
如图,一次函数的图象与反比例函数y1=" –" ( x<0)的图象相交于A点,与y轴、x轴分别相交于B、C两点,且C(2,0).当x<–1时,一次函数值大于反比例函数的值,当x>–1时,一次函数值小于反比例函数值.
(1)求一次函数的解析式;
(2)设函数y2= (x>0)的图象与y1=" –" (x<0)的图象关于y轴对称.在y2= (x>0)的图象上取一点P(P点的横坐标大于2),过P作PQ⊥x轴,垂足是Q,若四边形BCQP的面积等于2,求P点的坐标.
 |