如图1至图4中,两平行线AB、CD间的距离均为6,点M为AB上一定点.
思考:
如图1,圆心为0的半圆形纸片在AB,CD之间(包括AB,CD),其直径MN在AB上,MN=8,点P为半圆上一点,设∠MOP=α。
当α= 度时,点P到CD的距离最小,最小值为 。
探究一:
在图1的基础上,以点M为旋转中心,在AB,CD 之间顺时针旋转该半圆形纸片,直到不能再转动为止,如图2,得到最大旋转角∠BMO= 度,此时点N到CD的距离是 。
探究二:
将如图1中的扇形纸片NOP按下面对α的要求剪掉,使扇形纸片MOP绕点M在AB,CD之间顺时针旋转。
(1)如图3,当α=60°时,求在旋转过程中,点P到CD的最小距离,并请指出旋转角∠BMO的最大值;
(2)如图4,在扇形纸片MOP旋转过程中,要保证点P能落在直线CD上,请确定α的最大值。
如图,□ABCD中,点E、F分别在AD、BC上,且AE=CF.
求证:BE=DF.
如图所示,四边形ABCD中,AD∥BC,∠B=∠D,那么四边形ABCD是平行四边形吗?请说明理由.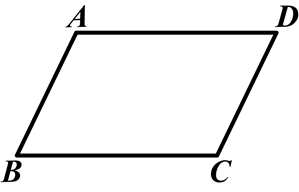
如图,四边形ABCD是平行四边形,∠EAD=∠BAF
(1)试说明:△CEF为等腰三角形;
(2)猜测CE与CF的和与□ABCD的周长有何关系,并说明理由.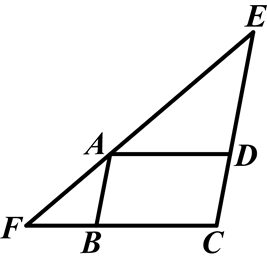
如图,AB∥EG,EF∥BC,AC∥FG,图中有几个平行四边形?将它们表示出来,并说明理由.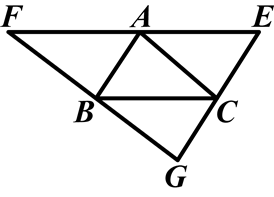
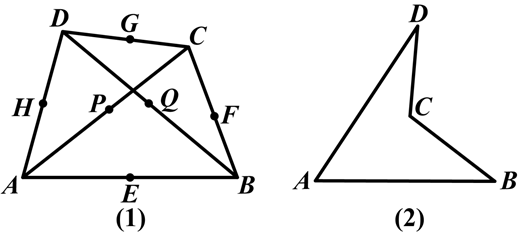
已知任意四边形ABCD,且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、G、H、P、Q.
(1)如图(1),判断下列结论是否正确(正确的在括号里填“√”,错误的在括号里填“×”):
甲:顺次连接EF、FG、GH、HE,一定得到平行四边形;( )
乙:顺次连接EQ、QG、GP、PE,一定得到平行四边形;( )
(2)请选择甲、乙中的一个,证明你对它的判断;
(3)如图(2),请你直接判断(1)中的两个结论是否成立.