如图,四边形ABCD是平行四边形,∠EAD=∠BAF
(1)试说明:△CEF为等腰三角形;
(2)猜测CE与CF的和与□ABCD的周长有何关系,并说明理由.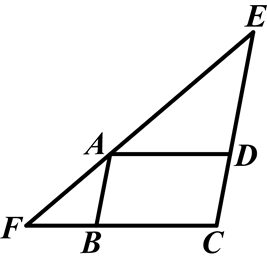
为倡导“低碳出行”,环保部门对某城市居民日常出行使用交通方式的情况进行了问卷调查,将调查结果整理后,绘制了如下不完整的统计图,其中“骑自行车、电动车”所在扇形的圆心角是162°.
请根据以上信息解答下列问题:
(1)本次调查共收回多少张问卷?
(2)补全条形统计图,在扇形统计图中,“其他”对应扇形的圆心角是度;
(3)若该城市有32万居民,通过计算估计该城市日常出行“骑自行车、电动车”和“坐公交车”的共有多少人?
在△ABC中,AB=AC=4,∠BAC=30°,以AC为一边作等边△ACD,连接BD.请画出图形,并直接写出△BCD的面积.
如图,抛物线y=x2+bx+c经过点A(﹣1,0),B(3,0).请解答下列问题:
(1)求抛物线的解析式;
(2)点E(2,m)在抛物线上,抛物线的对称轴与x轴交于点H,点F是AE中点,连接FH,求线段FH的长.
注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣ .
.
先化简:(x﹣ )÷
)÷ ,其中的x选一个适当的数代入求值.
,其中的x选一个适当的数代入求值.
如图,二次函数 的图象与x轴相交于点A(﹣3,0)、B(1,0),与y轴相交于点C,点G是二次函数图象的顶点,直线GC交x轴于点H(3,0),AD平行GC交y轴于点D.
的图象与x轴相交于点A(﹣3,0)、B(1,0),与y轴相交于点C,点G是二次函数图象的顶点,直线GC交x轴于点H(3,0),AD平行GC交y轴于点D.
(1)求该二次函数的表达式;
(2)求证:四边形ACHD是正方形;
(3)如图2,点M(t,p)是该二次函数图象上的动点,并且点M在第二象限内,过点M的直线 交二次函数的图象于另一点N.
交二次函数的图象于另一点N.
①若四边形ADCM的面积为S,请求出S关于t的函数表达式,并写出t的取值范围;
②若△CMN的面积等于 ,请求出此时①中S的值.
,请求出此时①中S的值.