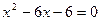一个四边形的周长是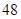 cm,已知第一条边的长是
cm,已知第一条边的长是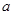 cm,第二条边长比第一条边长的
cm,第二条边长比第一条边长的 倍还少
倍还少 cm,第三条边长等于第一、第二条边长的和。请通过计算用含
cm,第三条边长等于第一、第二条边长的和。请通过计算用含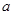 的代数式表示第四条边的长.
的代数式表示第四条边的长.
(本小题满分7分)
如图,在△ABC中,AB=AC,D为BC中点。四边形ABDE是平行四边形。
求证:四边形ADCE是矩形
(本小题满分5分)
如图,在△ABC中,点D、E分别在边AC、AB上,BD=CE,∠DBC=∠ECB。
求证:AB=AC
(本小题满分8分)
如图所示,小吴和小黄在玩转盘游戏,准备了两个可以自由转动的转盘甲、乙,每个转盘被分成面积相等的几个扇形区域,并在每个扇形区域内标上数字,游戏规则:同时转动两个转盘,当转盘停止转动后,指针所指扇形区域内的数字之和为4,5或6时,则小吴胜;否则小黄胜。(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一扇形区域为止)
(1)这个游戏规则对双方公平吗?说说你的理由;
(2)请你设计一个对双方都公平的游戏规则。
(本小题满分7分)
某中学七年级(8)班同学全部参加课外体育活动情况统计如图: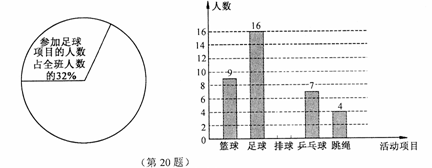
(1)请你根据以上统计图中的信息,填写下表:
| 该班人数 |
这五个活动项目人数的中位数 |
这五个活动项目人数的平均数 |
(2)请你将该条形统计图补充完整
(本小题满分10分)解方程:
(1) ;
;
(2)