掷两枚骰子,记事件A为“向上的点数之和为n”.
(1)求所有n值组成的集合;
(2)n为何值时事件A的概率P(A)最大?最大值是多少?
(3)设计一个概率为0.5的事件(不用证明)
已知(t2-4)10=a0+a1t+a2t2+a3t3+…a20t20
(1)求 的值
的值
(2)求
(3)求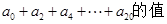 .
.
一个盒子里装有标号为1,2,3,…,n的n(n>3,且n∈N*)张标签,现随机地从盒子里无放回地抽取两张标签,记X为这两张标签上的数字之和,若X=3的概率为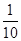 .
.
(1)求n的值;
(2)求X的分布列.
若 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.
(1)求n的值及展开式中二项式系数最大的项.
(2)此展开式中是否有常数项,为什么?
(本小题满分12分)用数学归纳法证明:当n为正整数时,13+23+33+……+n3=
已知函数
(1)求函数f(x)的极值
(2)求函数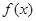 在
在 上的最大值和最小值.
上的最大值和最小值.