(本小题满分14分)
(本小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。(Ⅰ)将总费用y表示为x的函数
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用
(本小题满分13分)
如图,过抛物线 (
(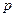 >0)的顶点作两条互相垂直的弦OA、OB。
>0)的顶点作两条互相垂直的弦OA、OB。
⑴设OA的斜率为k,试用k表示点A、B的坐标
⑵求弦AB中点M的轨迹方程
(本小题满分12分) 的极坐标方程分别为
的极坐标方程分别为
(Ⅰ)把 的极坐标方程化为直角坐标方程
的极坐标方程化为直角坐标方程
(Ⅱ)求经过 交点的直线的直角坐标方程
交点的直线的直角坐标方程
(本小题满分12分)
打鼾不仅影响别人休息,而且可能与患某种疾病有关,下表是一次调查所得数据,试问:每一晚都打鼾与患心脏病有关系吗?有多大把握认为你的结论成立?
| 患心脏病 |
未患心脏病 |
合计 |
|
| 每一晚都打鼾 |
46 |
30 |
76 |
| 不打鼾 |
20 |
50 |
70 |
| 合计 |
66 |
80 |
146 |