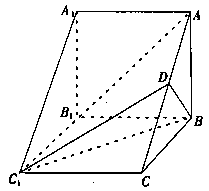
如图,在三棱柱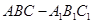 中,侧棱
中,侧棱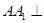 底面
底面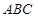 ,
,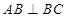 ,
,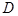 为
为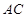 的中点,
的中点,
(1)求证: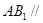 平面
平面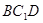 ;
;
(2)过点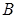 作
作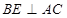 于点
于点 ,求证:直线
,求证:直线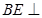 平面
平面
(3)若四棱锥 的体积为3,求
的体积为3,求 的长度
的长度
已知数列 满足
满足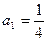 ,
, .
.
(1)试判断数列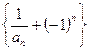 是否为等比数列,并说明理由;
是否为等比数列,并说明理由;
(2)设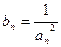 ,求数列
,求数列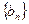 的前
的前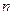 项和
项和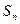 ;(3)设
;(3)设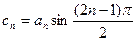 ,数列
,数列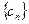 的前
的前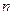 项和为
项和为 .求证:对任意的
.求证:对任意的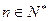 ,
,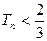 .
.
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中
是省外游客,其余是省内游客。在省外游客中有
持金卡,在省内游客中有
持银卡。
(Ⅰ)在该团中随机采访2名游客,求恰有1人持银卡的概率;
(Ⅱ)在该团中随机采访2名游客,求其中持金卡与持银卡人数相等的概率。
设数列
的前
项和为
,对任意的正整数
,都有
成立,记
.
(Ⅰ)求数列
与数列
的通项公式;
(Ⅱ)设数列
的前
项和为
,是否存在正整数
,使得
成立?若存在,找出一个正整数
;若不存在,请说明理由;
(Ⅲ)记
,设数列
的前
项和为
,求证:对任意正整数
都有
.
如图,正方形
所在平面与平面四边形
所在平面互相垂直,
是等腰直角三角形,
. 
(Ⅰ)求证:
平面
;
(Ⅱ)设线段
、
的中点分别为
、
,求证:
平面
;
(Ⅲ)求二面角 的大小.
设数列
的前n项和为
,对任意的正整数n,都有
成立,记
。
(Ⅰ)求数列
的通项公式;
(Ⅱ)记
,设数列
的前n项和为
,求证:对任意正整数n都有
;
(Ⅲ)设数列
的前n项和为
。已知正实数
满足:对任意正整数
恒成立,求
的最小值。