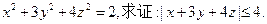在等差数列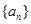 和等比数列
和等比数列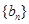 中,
中,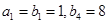 ,
,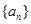 的前10项和
的前10项和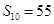 .
.
(1)求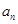 和
和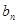 ;
;
(2)现分别从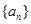 和
和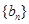 的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.
的前3项中各随机抽取一项,写出相应的基本事件,并求这两项的值相等的概率.
((本小题满分12分)
已知四棱锥 中
中 平面
平面 ,且
,且 ,底面为直角梯形,
,底面为直角梯形,

 分别是
分别是 的中点.
的中点.
(1)求证: // 平面
// 平面 ;
;
(2)求截面 与底面
与底面 所成二面角的大小;
所成二面角的大小;
(3)求点 到平面
到平面 的距离.
的距离.
((本小题满分12分)
设不等式 确定的平面区域为
确定的平面区域为 ,
, 确定的平面区域为
确定的平面区域为 .
.
(1)定义横、纵坐标为整数的点为“整点”,在区域 内任取3个整点,求这些整点中恰有2个整点在区域
内任取3个整点,求这些整点中恰有2个整点在区域 的概率;
的概率;
(2)在区域 内任取3个点,记这3个点在区域
内任取3个点,记这3个点在区域 的个数为
的个数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)
设数列 满足
满足 且对一切
且对一切 ,有
,有 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设  ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)
已知 为坐标原点,
为坐标原点, 其中
其中 为常数,设函数
为常数,设函数 .
.
(1)求函数 的表达式和最小正周期;
的表达式和最小正周期;
(2)若角 为
为 的三个内角中的最大角且
的三个内角中的最大角且 的最小值为
的最小值为 ,求
,求 的值;
的值;
(3)在(2)的条件下,试画出 的简图.
的简图.
((本小题满分10分)
已知