分解因式:(1) ;(2)
;(2) .
.
先化简,再求值: ,其中
,其中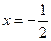
已知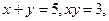 则
则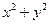 =""
=""
(1)如图,OA=2, P为y轴负半轴上一个动点,当P点沿y轴负半轴向下运动时,以P为顶点,PA为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP-DE的值.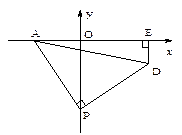
(2)如图,已知点F坐标为(-2,-2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,以下两个结论:①m—n为定值;②m+n为定值,其中只有一个结论是正确的,请找出正确的结论,并求出其值. 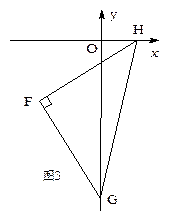
康乐公司在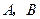 两地分别有同型号的机器
两地分别有同型号的机器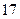 台和
台和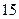 台,现要运往甲地
台,现要运往甲地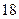 台,乙地
台,乙地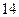 台,从
台,从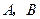 两地运往甲、乙两地的费用如下表:
两地运往甲、乙两地的费用如下表:
| 甲地(元/台) |
乙地(元/台) |
|
| 地 |
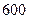 |
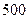 |
| 地 |
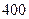 |
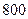 |
(1)如果从地运往甲地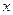 台,求完成以上调运所需总费用
台,求完成以上调运所需总费用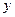 (元)与
(元)与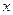 (台)之间的函数关系式;
(台)之间的函数关系式;
(2)请你为康乐公司设计一种最佳调运方案,使总费用最少,并说明理由