已知△ABC的一条边BC的长为5,另两边AB、AC的长是关于x的一元二次方程x2-(2k+3) x+k2+3k+2=0的两个实数根.
(1)求证:无论k为何值时,方程总有两个不相等的实数根.
(2)k为何值时,△ABC是以BC为斜边的直角三角形.
列方程解应用题:八年级学生到距离学校15千米的农科所参观,一部分学生骑自行车先走,走了40分钟后,其余同学乘汽车出发,结果两者同时到达.若汽车的速度是骑自行车同学速度的3倍,求骑自行车同学的速度.
如图,在平面直角坐标系中,每个小正方形的边长为1,点A的坐标为(-3,2)。
请按要求分别完成下列各小题:
(1)画出△ABC关于y轴对称的△ ,则点
,则点 的坐标是;
的坐标是;
(2)△ABC的面积是。
如图所示,在△ABC中,AB=AC,DE垂直平分AB于点E,交AC于点D,若△ABC的周长为26,BC=6,求△BCD的周长.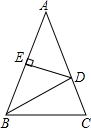
如图所示,在△ABC中,AE、BF是角平分线,它们相交于点O,AD是高,∠BAC=50°,∠C=70°,求∠DAC、∠BOA的度数.
如图,已知:EC=AC,∠BCE=∠DCA,∠A=∠E。求证:∠B=∠D.