把下列各数填入它所属的集合内:
15,-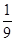 ,-5,
,-5,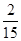 ,0,-5.32,2.
,0,-5.32,2.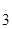 .
.
(1)分数集合{ . . .};
(2)整数集合{ . . .}。
如图,已知直线l经过点A(1,0),与双曲线y=
(x>0)交于点B(2,1).过点P(p,p-1)(p>1)作x轴的平
行线分别交双曲线y=(x>0)和y=-(x<0)于点M、N.
(1)求m的值和直线l的解析式;
(2)若点P在直线y=2上,求证:△PMB∽△PNA;
(3)是否存在实数p,使得S△AMN=4S△AMP?若存在,请求出所有满足条件的p的值;若
不存在,请说明理由.
(12分)已知A(1,0)、B(0,-1)、C(-1,2)、D(2,-1)、E(4,2)五个点,抛物线y=a(x-1)2+k(a>0)经过其中的三个点.
(1)求证:C、E两点不可能同时在抛物线y=a(x-1)2+k(a>0)上;
(2)点A在抛物线y=a(x-1)2+k(a>0)上吗?为什么?
(3)求a和k的值.
(10分)如图1,O为正方形ABCD的中心,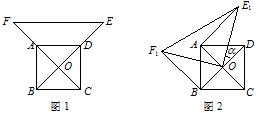
分别延长OA、OD到点F、E,使OF=2OA,
OE=2OD,连接EF.将△EOF绕点O逆时针
旋转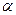 角得到△E1OF1(如图2).
角得到△E1OF1(如图2).
(1)探究AE1与BF1的数量关系,并给予证明;
(2)当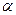 =30°时,求证:△AOE1为直角三角形.
=30°时,求证:△AOE1为直角三角形.
(8分)比较正五边形与正六边形,可以发现它们的相同点和不同点.例如: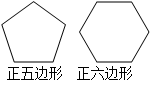
它们的一个相同点:正五边形的各边相等,正六边形的各边也相等.
它们的一个不同点:正五边形不是中心对称图形,正六边形是中心对称图形.
请你再写出它们的两个相同点和不同点:
相同点:
①;
②.
不同点:
①;
②.
(8分)在社区全民健身活动中,父子俩参加跳绳比赛.相同时间内父亲跳180个,儿子跳210个.已知儿子每分钟比父亲多跳20个,父亲、儿子每分钟各跳多少个?