某校数学活动小组随机调查学校住在校外的100名同学的上学方式,根据调查统计结果,按“步行”、“骑自行车”和“其他”三类汇总分析,并制成条形统计图和扇形统计图(如图所示).
(1)请你补全条形统计图和扇形统计图;
(2)求出扇形统计图中“步行”部分的圆心角的度数;
(3)学校正在规划新的学生自行车停车场,一般情况下,5辆自行车占地2m2,另有自行车停放总面积的作为通道.若全校共有1200名同学住在校外,那么请你估计,学校应当规划至少多大面积的学生自行车停车场?(骑自行车的学生按每人骑一辆计算)
如图,某建筑物AC顶部有一旗杆AB,且点A,B,C在同一条直线上,小明在地面D处观测旗杆顶端B的仰角为30°,然后他正对建筑物的方向前进了20米到达地面的E处,又测得旗杆顶端B的仰角为60°,已知建筑物的高度 ,求旗杆AB的高度(结果精确到0.1米).参考数据: .

求不等式组 的解集,并把它们的解集在数轴上表示出来.
已知:如图,在四边形ABCD中, ,E是BC的中点,直线AE交DC的延长线于点F.试判断四边形ABFC的形状,并证明你的结论.
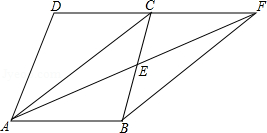
在读书月活动中,某校号召全体师生积极捐书,为了解所捐书籍的种类,图书管理员对部分书籍进行了抽样调查,根据调查数据绘制了如下不完整的统计图表.请你根据统计图表所提供的信息回答下面问题:
某校师生捐书种类情况统计表
|
种类 |
频数 |
百分比 |
|
A.科普类 |
12 |
n |
|
B.文学类 |
14 |
35% |
|
C.艺术类 |
m |
20% |
|
D.其它类 |
6 |
15% |
(1)统计表中的m= ,n= ;
(2)补全条形统计图;
(3)本次活动师生共捐书2000本,请估计有多少本科普类图书?
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为 、 、 (正方形网格中每个小正方形的边长是1个单位长度).
(1)△A1B1C1是△ABC绕点 逆时针旋转 度得到的,B1的坐标是 ;
(2)求出线段AC旋转过程中所扫过的面积(结果保留π).