李明上星期买进某公司股票7000股，每股27元，下表为本周每日该股票的涨跌情况（单位：元）
| 星期 |
一 |
二 |
三 |
四 |
五 |
六 |
| 每股涨跌 |
+4 |
+4.5 |
 |
 |
 |
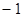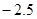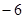+2 |
（1） 这六天中，哪几天的股票是上涨的？哪几天的股票是下跌的？
（2）哪天股票上涨的最多？你能算出这天收盘时每股是多少元吗？
探索与研究：
方法1：如图（a），对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得，所以
∠BAE＝90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图示写出证明勾股定理的过程；
方法2：如图（b），是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？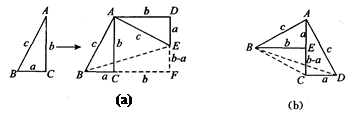
如图，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上.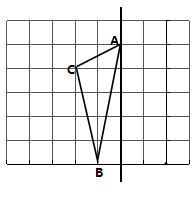
（1）在图中画出与△ABC关于直线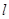
成轴对称的△A
；
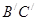（2）线段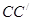
被直线；
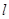（3）在直线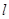上找一点P，使PB+PC的长最短，并算出这个最短长度.
已知，如图，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．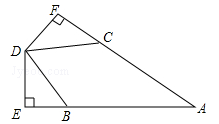
（1）已知x＝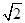
－1，求x2＋3x－1的值；
（2）已知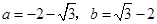
，求
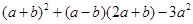值.
已知一次函数y=kx+b的图象经过点（-1，-5），且与正比例函数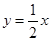
的图象相交于点（2，a）．
（1）求a的值．
（2）求一次函数y=kx+b的表达式．
（3）在同一坐标系中，画出这两个函数的图象．