探索与研究:
方法1:如图(a),对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得,所以
∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图示写出证明勾股定理的过程;
方法2:如图(b),是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?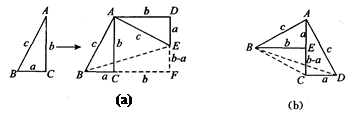
(10分)已知一次函数的图象与反比例函数的图象交于点A(3,2)、B(-2, m).
(1)求这两个函数的关系式,并在同一坐标系(如图7)中画出这 两个函数的图象;
两个函数的图象;
(2)观察(1)中两个函数的图象,写出使一次函数的值大于反比例函数的值时,自变量x的取值范围.
(8分) 某市为治理污水,需要铺设一段全长为300米的污水排放管道.铺设120米后,为了尽量减少施工对城市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用15天完成这一任务.求原计划每天铺设管道的长度.
(6分) 解方程: .
.
计算(每小题6分,共12分)
(1) ;(2)
;(2) .
.
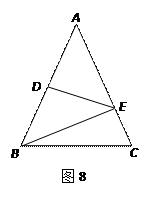
如图8,在 △ABC中,∠A=50°,∠C=65°,AB=12,BC=10,DE垂直平分AB交AC、AB于E、D两点.
△ABC中,∠A=50°,∠C=65°,AB=12,BC=10,DE垂直平分AB交AC、AB于E、D两点.
求:(1)∠EBC的度数;(2)△BCE的周长.