(1)用配方法把二次函数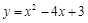 化为顶点式,并在直角坐标系中画出它的大致图象(
化为顶点式,并在直角坐标系中画出它的大致图象( ).
).
(2)若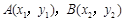 是函数
是函数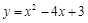 图象上的两点,且
图象上的两点,且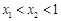 ,请比较
,请比较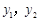 的大小关系.(直接写结果)
的大小关系.(直接写结果)
(3)把方程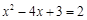 的根在函数
的根在函数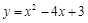 的图象上表示出来.
的图象上表示出来.
如图,在等腰Rt△ABC与等腰Rt△DBE中,∠BDE=∠ACB=90°,且BE在AB边上,取AE的中点F,CD的中点G,连结GF.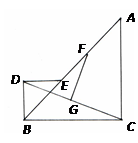
(1)FG与DC的位置关系是 ,FG与DC的数量关系是 ;
(2)若将△BDE绕B点逆时针旋转180°,其它条件不变,请完成下图,并判断(1)中的结论是否仍然成立? 请证明你的结论.
为预防甲型H1N1流感,某校对教室喷洒药物进行消毒.已知喷洒药物时每立方米空气中的含药量y(毫克)与时间x(分钟)成正比,药物喷洒完后,y与x成反比例(如图所示).现测得10分钟喷洒完后,空气中每立方米的含药量为8毫克.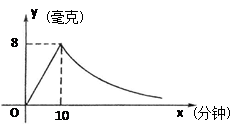
(1)求喷洒药物时和喷洒完后,y关于x的函数关系式;
(2)若空气中每立方米的含药量低于2毫克学生方可进教室,问消毒开始后至少要经过多少分钟,学生才能回到教室?
(3)如果空气中每立方米的含药量不低于4毫克,且持续时间不低于10分钟时,才能杀灭流感病毒,那么此次消毒是否有效?为什么?
如图,以△ABC的三边为边,在BC的同侧作三个等边△ABD、△BEC、△ACF.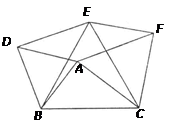
(1)判断四边形ADEF的形状,并证明你的结论;
(2)当△ABC满足什么条件时,四边形ADEF是菱形?是矩形?
小军八年级上学期的数学成绩如下表所示:
| 测验 类别 |
平时 |
期中 考试 |
期末 考试 |
|||
| 测验1 |
测验2 |
测验3 |
测验4 |
|||
| 成绩 |
110 |
105 |
95 |
110 |
108 |
112 |
(1)计算小军上学期平时的平均成绩;
(2)如果学期总评成绩按扇形图所示的权重计算,问小军上学期的总评成绩是多少分?
如图,已知一次函数y=k1x+b的图象与反比例函数y=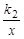 的图象交于A(1,-3),B(3,m)两点,连接OA、OB.
的图象交于A(1,-3),B(3,m)两点,连接OA、OB.
(1)求两个函数的解析式;(2)求△AOB的面积.