(本小题满分10分).
(选修4-1) 如图,在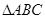 中,
中, ,以
,以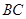 为直径的圆
为直径的圆 交
交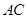 于点
于点 ,设
,设 为
为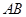 的中点.
的中点.
(I)求证:直线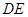 为圆
为圆 的切线;
的切线;
(Ⅱ)设 交圆
交圆 于点
于点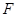 ,求证:
,求证:
已知 ,
,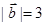 ,
,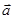 与
与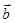 的夹角为
的夹角为 .
.
求(1) ;(2)
;(2) .
.
若 ,
, 是第四象限角,求
是第四象限角,求 的值.
的值.
为了参加奥运会,对自行车运动员甲、乙两人在相同的条件下进行了6次测试,测得他们的最大速度的数据如表所示:
| 甲 |
27 |
38 |
30 |
37 |
35 |
31 |
| 乙 |
33 |
29 |
38 |
34 |
28 |
36 |
(1)分别求甲、乙两运动员最大速度
的平均数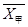 ,
,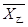 及方差
及方差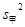 ,
, ;
;
(2)根据(1)所得数据阐明:谁参加这项重大比赛更合适.
(本小题满分14分)已知函数 .
.
(Ⅰ)若函数 为偶函数,求
为偶函数,求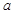 的值;
的值;
(Ⅱ)若 ,求函数
,求函数 的单调递增区间;
的单调递增区间;
(Ⅲ)当 时,若对任意的
时,若对任意的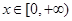 ,不等式
,不等式 恒成立,求实数
恒成立,求实数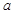 的取值范围.
的取值范围.
(本小题满分14分)已知半径为2,圆心在直线 上的圆C.
上的圆C.
(Ⅰ)当圆C经过点A(2,2)且与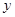 轴相切时,求圆C的方程;
轴相切时,求圆C的方程;
(Ⅱ)已知E(1,1),F(1,-3),若圆C上存在点Q,使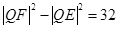 ,求圆心的横坐标
,求圆心的横坐标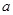 的取值范围.
的取值范围.