甲、乙两个港口相距72千米,一艘轮船从甲港出发,顺流航行3小时到达乙港,休息1小时后立即返回;一艘快艇在轮船出发2小时后从乙港出发,逆流航行2小时到甲港,并立即返回(掉头时间忽略不计)。已知水流速度是2千米/时,下图表示轮船和快艇距甲港的距离y(千米)与轮船出发时间x(小时)之间的函数关系式,结合图象解答下列问题:
(顺流速度=船在静水中速度+水流速度;逆流速度=船在静水中速度-水流速度) 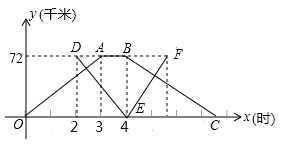
(1)轮船在静水中的速度是 千米/时;快艇在静水中的速度是 千米/时;
(2)求快艇返回时的解析式,写出自变量取值范围;
(3)快艇出发多长时间,轮船和快艇在返回途中相距12千米?(直接写出结果)
如图,是一辆小汽车沿一条高速公路匀速前进的时间t(小时)与速度x(千米/时)关系的图象,根据图象提供的信息回答下列问题: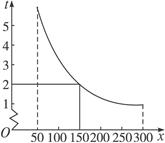
(1)这条高速公路的全长是多少千米?
(2)写出速度与时间之间的函数关系.
(3)汽车最大速度可以达到多少?
(4)汽车最慢用几个小时可以到达?如果要在3小时以内到达,汽车的速度应不少于多少?
反比例函数y= 的图象经过点A(4,-2),
的图象经过点A(4,-2),
(1)求这个函数的解析式;
(2)请判断点B(1,8)是否在这个反比例函数的图象上,并说明理由.
△ABC是锐角三角形,BC=6,面积为12.点P在AB上,点Q在AC上.如图9-33,正方形PQRS(RS与A在PQ的异侧)的边长为x,正方形PQRS与△ABC的公共部分的面积为y.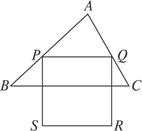
(1)当RS落在BC上时,求x;
(2)当RS不落在BC上时,求y与x的函数关系式;
(3)求公共部分面积的最大值.
某商店经销一种销售成本为每千克40元的水产品.根据市场分析,若按每千克50元销售,一个月能销售500千克;销售单价每涨1元,月销售量就减少10千克.针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克x元,月销售利润为y元,求y与x之间的函数关系式;
(3)商店想在月销售成本不超过10 000元的情况下,使得月销售利润达到5 000元,销售单价应定为多少?
如图,正方形ABCD边长是16 cm,P是AB上任意一点(与A、B不重合),QP⊥DP.设AP="x" cm,BQ="y" cm.试求出y与x之间的函数关系式.