(几何证明选讲选做题)如图,PC切⊙O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,PC=4,PB=8,则CD=___________.
已知正四棱锥P-ABCD的侧棱与底面所成角为60°,M为PA中点,连接DM,则DM与平面PAC所成角的大小是________.
如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,AA1=2,AC=BC=1,则异面直线A1B与AC所成角的余弦值是________.
已知ABCD-A1B1C1D1为正方体,①(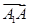 +
+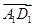 +
+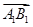 )2=3
)2=3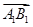 2;②
2;②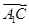 ·(
·(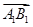 -
-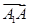 )=0;③向量
)=0;③向量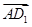 与向量
与向量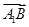 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|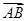 ·
·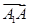 ·
·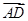 |.其中正确命题的序号是________.
|.其中正确命题的序号是________.
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABC.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是________.
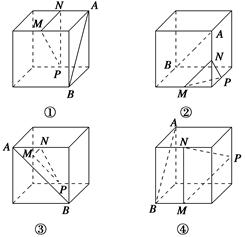
下列四个正方体中,A,B为正方体的两个顶点,M,N,P分别为其所在棱的中点,能得出直线AB∥平面MNP的图形的序号是________(写出所有符合要求的图形序号).