已知函数
(1)求函数 的单调递增区间;
的单调递增区间;
(2)记函数 的图象为曲线C.设点A(x1,y1),B(x2,y2)是曲线C上的不同两
的图象为曲线C.设点A(x1,y1),B(x2,y2)是曲线C上的不同两
点.如果在曲线C上存在点M(x0,y0),使得:① ;②曲线C在点M处的切线
;②曲线C在点M处的切线
平行于直线AB,则称函数F(x)存在“中值相依切线”,试问:函数f(x)是否存在“中
值相依切线”,请说明理由.
设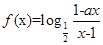 为奇函数,
为奇函数,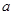 为常数,
为常数,
(1)求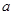 的值;
的值;
(2)证明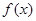 在区间
在区间 上单调递增;
上单调递增;
(3)若 ,不等式
,不等式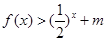 恒成立,求实数
恒成立,求实数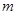 的取值范围。
的取值范围。
已知向量
 ,函数
,函数
(1)求函数 的最小正周期;
的最小正周期;
(2)已知 分别为△ABC内角A,B,C的对边,
分别为△ABC内角A,B,C的对边, ,且
,且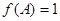 ,求A和△ABC面积的最大值。
,求A和△ABC面积的最大值。
在 中,
中,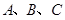 是三角形的三内角,
是三角形的三内角,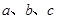 是三内角对应的三边,已知
是三内角对应的三边,已知 。
。
(1)求角 的大小;
的大小;
(2)若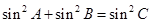 ,求角
,求角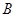 的大小。
的大小。
已知函数 。
。
(1)若 的解集为
的解集为 ,求实数
,求实数 的值。
的值。
(2)当 且
且 时,解关于
时,解关于 的不等式
的不等式 。
。
在平面直角坐标系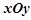 中,曲线
中,曲线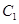 为
为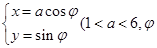 为参数)。在以
为参数)。在以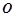 为原点,
为原点,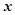 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线 的极坐标方程为
的极坐标方程为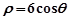 ,射线为
,射线为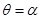 ,与
,与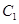 的交点为
的交点为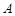 ,与
,与 除极点外的一个交点为
除极点外的一个交点为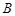 。当
。当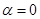 时,
时,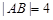 。
。
(1)求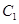 ,
, 的直角坐标方程;
的直角坐标方程;
(2)设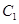 与
与 轴正半轴交点为
轴正半轴交点为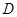 ,当
,当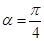 时,设直线
时,设直线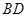 与曲线
与曲线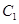 的另一个交点为
的另一个交点为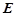 ,求
,求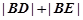 。
。