如图,正方形ABCD和三角形ACE所在的平面互相垂直.EF∥BD,AB= EF.求证:
EF.求证:
(1)BF∥平面ACE;
(2)BF⊥BD.
已知函数 ,其中
,其中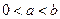 ,
,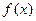 在
在 及
及 处取得极值,其中
处取得极值,其中 .
.
(1)求证: ;
;
(2)求证:点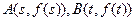 的中点
的中点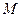 在曲线
在曲线 上.
上.
已知数列 中,
中,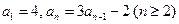 .
.
(1)求数列 的通项公式
的通项公式 ;
;
(2)证明: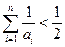 .
.
设抛物线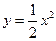 的焦点为F,准线为
的焦点为F,准线为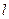 ,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
,过点F作一直线与抛物线交于A、B两点,再分别过点A、B作抛物线的切线,这两条切线的交点记为P.
(1)证明:直线PA与PB相互垂直,且点P在准线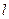 上;
上;
(2)是否存在常数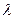 ,使等式
,使等式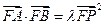 恒成立?若存在,求出
恒成立?若存在,求出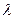 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知数列 的前
的前 项和为
项和为 ,
, ,且
,且 .
.
(1)计算 ;
;
(2)猜想 的表达式,并证明.
的表达式,并证明.
在直四棱柱ABCD—A1B1C1D1中,已知底面四边形
ABCD是边长为3的菱形,且DB=3,A1A=2,点E
在线段BC上,点F在线段D1C1上,且BE=D1F=1.
(1)求证:直线EF∥平面B1D1DB;
(2)求二面角F—DB—C的余弦值.