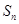某地高三“调考”数学第1卷中共有8道选择题,每道选择题有4个选项,其中只有一个是正确的;评分标准规定:“每题只选一项,答对得5分,不答或答错行0分.”某考生每道题都给出一个答案.已确定5道题的答案是正确的,而其余选择题中有1道题可判断出两个选项是错误的,有一道要可以判断出一个选项是错误的,还有一道因不了解题意只能乱猜,试求出该考生:
(1)得40分的概率; (2)得多少分的可能性最大? (3)所得分数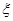 的数学期望.
的数学期望.
(本小题满分14分)
已知椭圆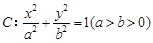 的离心率为
的离心率为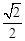 ,其中左焦点F(-2,0).
,其中左焦点F(-2,0).
(1) 求椭圆C的方程;
(2) 若直线y=x+m与椭圆C交于不同的两点A,B,且线段AB的中点M在圆x2+y2=1上,
求m的值.
(本小题满分14分)
如图,正三棱柱 中,
中,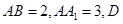 为
为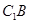
的中点,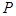 为
为 边上的动点.
边上的动点.
(Ⅰ)当点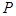 为
为 的中点时,证明DP//平面
的中点时,证明DP//平面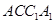 ;
;
(Ⅱ)若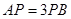 ,求三棱锥
,求三棱锥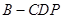 的体积.
的体积.
(本小题满分14分)
已知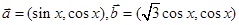 ,设函数
,设函数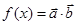
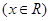
|
(1)求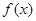 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
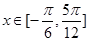 时,求
时,求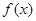 的值域.
的值域.
(本小题满分12分)
在△ABC中,角A、B、C所对边分别为a,b,c,已知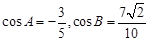 ,
,
(1)求角C的大小;
(2)若最长边的边长为l0 ,求△ABC的面积.
(本小题满分12分)
设递增等差数列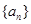 的前项和为
的前项和为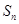 ,已知
,已知 ,
, 是
是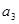 和
和 的等比中项。
的等比中项。
(1)求数列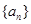 的通项公式;
的通项公式;
(2)求数列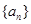 的前项和
的前项和