已知函数
的图像在点
处的切线方程为
.
(Ⅰ)求实数
的值;
(Ⅱ)设
是
上的增函数.
(ⅰ)求实数
的最大值;
(ⅱ)当
取最大值时,是否存在点Q,使得过点Q的直线能与曲线
围成两个封闭图形,则这两个封闭图形的面积总相等?若存在,求出点Q的坐标;若不存在,说明理由.
某港口
要将一件重要物品用小艇送到一艘正在航行的轮船上,在小艇出发时,轮船位于港口的
北偏西30°且与该港口相距20海里的
处,并正以30海里/小时的航行速度沿正东方向匀速行驶。假设该小艇沿直线方向以
海里/小时的航行速度匀速行驶,经过
小时与轮船相遇.
(I)若希望相遇时小艇的航行距离最小,则小艇航行速度的大小应为多少?
(II)为保证小艇在30分钟内(含30分钟)能与轮船相遇,试确定小艇航行速度的最小值;
(III)是否存在
,使得小艇以v海里/小时的航行速度行驶,总能有两种不同的航行方向与轮船相遇?若存在,试确定v的取值范围;若不存在,请说明理由.
如图,在长方体
中,
分别是棱
上的点(点
与
不重合),且
. 过
的平面与棱
相交,交点分别为
. 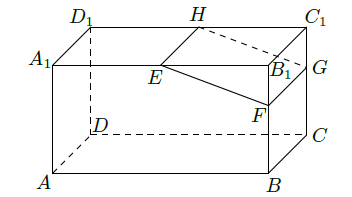
(I)证明: 平面 ;
(II)设 .在长方体 内随机选取一点.记该点取自几何体 内的概率为 ,当点 分别在棱 上运动且满足 时,求 的最小值.
已知抛物线
的方程
过点
.
(I)求抛物线
的方程,并求其准线方程;
(II)是否存在平行于
(O为坐标原点)的直线
,使得直线
与抛物线
有公共点,且直线
与
的距离等于
?若存在,求出直线
的方程;若不存在,说明理由。
设平面向量
,其中
.
(I)请列出有序数组
的所有可能结果;
(II)记"使得
成立的
"为事件
,求事件
发生的概率.