(本小题满分l2分)已知{an}的前n项和 (其中
(其中 ),且Sn的最大值为9。
),且Sn的最大值为9。
(1)确定常数k的值,并求数列{an}的通项公式;
(2)求数列 的前n项和
的前n项和 。
。
某人上午7:00时,乘摩托车以匀速 千米/时
千米/时 从A地出发到相距50千米的
从A地出发到相距50千米的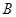 地去,然后乘汽车以匀速
地去,然后乘汽车以匀速 千米/时
千米/时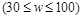 自
自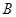 地向相距300千米的C地驶去,要求在当天16:00时至21:00时这段时间到达C地.设汽车所需要的时间为
地向相距300千米的C地驶去,要求在当天16:00时至21:00时这段时间到达C地.设汽车所需要的时间为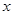 小时, 摩托车所需要的时间为
小时, 摩托车所需要的时间为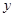 小时.
小时.
(1)写出满足上述要求的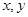 的约束条件;
的约束条件;
(2)如果途中所需的经费为 ,且
,且 (元),那么
(元),那么 ,
,  分别是多少时所要的经费最少?此时需花费多少元?
分别是多少时所要的经费最少?此时需花费多少元?
已知向量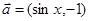
 ,函数
,函数
(1)求函数 的值域;
的值域;
(2)已知 分别为△ABC内角A,B,C的对边,
分别为△ABC内角A,B,C的对边, ,且
,且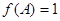 ,求A和△ABC面积的最大值。
,求A和△ABC面积的最大值。
某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组 ;第二组
;第二组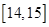 ……第五组
……第五组 .下图是按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.
(I)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(II)设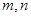 表示该班某两位同学的百米测试成绩,且已知
表示该班某两位同学的百米测试成绩,且已知 求事件
求事件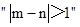 的概率.
的概率.
在△ABC中,已知B=45°,D是BC边上的一点,AD="10," AC=14,DC=6,求AB的长.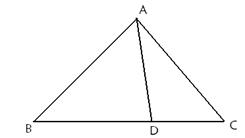
求值: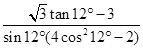 .
.