某人上午7:00时,乘摩托车以匀速 千米/时
千米/时 从A地出发到相距50千米的
从A地出发到相距50千米的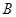 地去,然后乘汽车以匀速
地去,然后乘汽车以匀速 千米/时
千米/时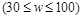 自
自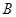 地向相距300千米的C地驶去,要求在当天16:00时至21:00时这段时间到达C地.设汽车所需要的时间为
地向相距300千米的C地驶去,要求在当天16:00时至21:00时这段时间到达C地.设汽车所需要的时间为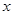 小时, 摩托车所需要的时间为
小时, 摩托车所需要的时间为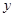 小时.
小时.
(1)写出满足上述要求的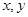 的约束条件;
的约束条件;
(2)如果途中所需的经费为 ,且
,且 (元),那么
(元),那么 ,
,  分别是多少时所要的经费最少?此时需花费多少元?
分别是多少时所要的经费最少?此时需花费多少元?
已知数列 的前
的前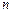 项和为
项和为 ,
, ,
, (
(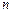 为正整数).
为正整数).
(1)求数列 的通项公式;
的通项公式;
(2)记 ,若对任意正整数
,若对任意正整数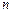 ,
, 恒成立,求
恒成立,求 的取值范围?
的取值范围?
(3)已知集合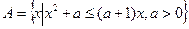 ,若以a为首项,a为公比的等比数列前n项和记为
,若以a为首项,a为公比的等比数列前n项和记为 ,问是否存在实数a使得对于任意的
,问是否存在实数a使得对于任意的 .若存在,求出a的取值范围;若不存在,说明理由.
.若存在,求出a的取值范围;若不存在,说明理由.
已知点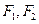 是双曲线M:
是双曲线M: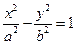 的左右焦点,其渐近线为
的左右焦点,其渐近线为 ,且右顶点到左焦点的距离为3.
,且右顶点到左焦点的距离为3.
(1)求双曲线M的方程;
(2) 过 的直线
的直线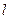 与M相交于
与M相交于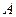 、
、 两点,直线
两点,直线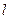 的法向量为
的法向量为 ,且
,且 ,求k的值;
,求k的值;
(3)在(2)的条件下,若双曲线M在第四象限的部分存在一点C满足 ,求m的值及△ABC的面积
,求m的值及△ABC的面积 .
.
已知函数 (k为常数),
(k为常数), 是函数
是函数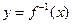 图像上的点.
图像上的点.
(1)求实数k的值及函数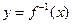 的解析式;
的解析式;
(2)将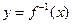 的图像按向量
的图像按向量 平移得到函数y=g(x)的图像.
平移得到函数y=g(x)的图像.
若 对任意的
对任意的 恒成立,试求实数m的取值范围.
恒成立,试求实数m的取值范围.
已知函数 .
.
(1)将f(x)写成 (
(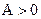 )的形式,并求其图像对称中心的横坐标;
)的形式,并求其图像对称中心的横坐标;
(2)如果△ABC的三边a、b、c满足 ,且边b所对的角为x,试求x的取值范围及此时函数f(x)的值域.
,且边b所对的角为x,试求x的取值范围及此时函数f(x)的值域.
已知函数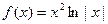 ,
,
(Ⅰ)判断函数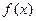 的奇偶性;
的奇偶性;
(Ⅱ)求函数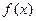 的单调区间;
的单调区间;
(Ⅲ)若关于 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围.
的取值范围.