直线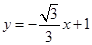 和
和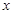 轴,
轴,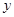 轴分别交于点
轴分别交于点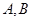 ,以线段
,以线段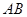 为边在第一象限
为边在第一象限
内作等边△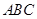 ,如果在第一象限内有一点
,如果在第一象限内有一点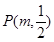 使得△
使得△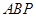 和△
和△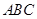 的面积相等,
的面积相等,
求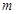 的值。
的值。
(本小题满分12分)
已知函数 .
.
(1)若函数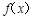 在(
在(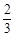 ,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
,1)上单调递减,在(1,+∞)上单调递增,求实数a的值;
(2)是否存在正整数a,使得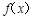 在(
在(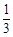 ,
, )上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
)上既不是单调递增函数也不是单调递减函数?若存在,试求出a的值,若不存在,请说明理由.
(本小题满分12分已知 的内角
的内角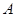 、
、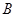 、
、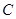 的对边分别为
的对边分别为 、
、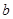 、
、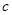 ,
,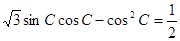 ,且
,且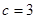
(1)求角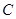 ;
;
(2)若向量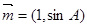 与
与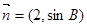 共线,求
共线,求 、
、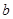 的值.
的值.
(本小题满分12分)
已知 ,设
,设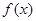 =
=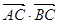 (1).求
(1).求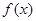 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)设关于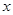 的方程
的方程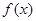 =
=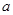 在
在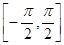 有两个不相等的实数根,求
有两个不相等的实数根,求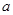 的取值范围.
的取值范围.
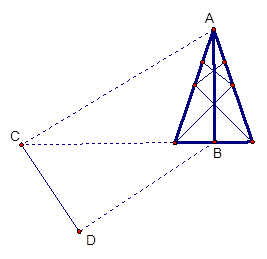
(10分) 测量河对岸的塔高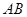 时,可以选与塔底
时,可以选与塔底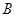 在同一水平面内的两个测点
在同一水平面内的两个测点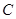 与
与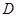 .现测得
.现测得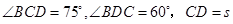 ,并在点
,并在点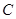 测得塔顶
测得塔顶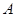 的仰角为
的仰角为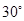 ,求塔高
,求塔高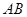 。
。
设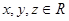 且
且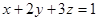 .
.
(I)当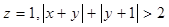 时,求实数
时,求实数 的取值范围;
的取值范围;
(II)当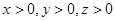 时,求
时,求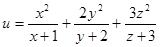 的最小值.
的最小值.