设函数f(x)是(－∞，＋∞)上的减函数，则( )
| A．f(a)>f(2a) | B．f(a2)<f(a) |
| C．f(a2＋a)<f(a) | D．f(a2＋1)<f(a) |
用数学归纳法证明“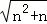
＜n+1 （n∈N*）”．第二步证n=k+1时（n=1已验证，n=k已假设成立），这样证明：
=
＜
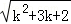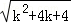=（k+1）+1，所以当n=k+1时，命题正确．此种证法（）
| A．是正确的 |
| B．归纳假设写法不正确 |
| C．从k到k+1推理不严密 |
| D．从k到k+1推理过程未使用归纳假设 |
在数学归纳法证明多边形内角和定理时，第一步应验证（）
| A．n=1成立 | B．n=2成立 | C．n=3成立 | D．n=4成立 |
设f（n）=
+
+
+…+
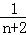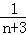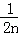（n∈N*），那么f（n+1）﹣f（n）等于（）
A． |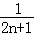
B． |
C．+ |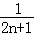
D．﹣ |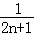
利用独立性检验来考虑两个分类变量X和Y是否有关系时，通过查阅下表来确定断言“X和Y有关系”的可信度，如果k＞5.024，那么就有把握认为“X和Y有关系”的百分比为（）
| P（K2＞k） |
0.50 |
0.40 |
0.25 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
| k |
0.455 |
0.708 |
1.323 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
A.25% B.75% C.2.5% D.97.5%
高二第二学期期中考试，按照甲、乙两个班级学生数学考试成绩优秀和不优秀统计后，得到如表：
班组与成绩统计表
| 优秀 |
不优秀 |
总计 |
|
| 甲班 |
11 |
34 |
45 |
| 乙班 |
8 |
37 |
45 |
| 总计 |
19 |
71 |
90 |
则随机变量K2的观测值约为（）
A.0.600 B.0.828 C.2.712 D.6.004