我国发射的“嫦娥一号”探月卫星沿近似于圆形的轨道绕月飞行.为了获得月球表面全貌的信息,让卫星轨道平面缓慢变化.卫星将获得的信息持续用微波信号发回地球.设地球和月球的质量分别为M和m,地球和月球的半径分别为R和R1,月球绕地球的轨道半径和卫星绕月球的轨道半径分别为r和r1,月球绕地球转动的周期为T.假定在卫星绕月运行一个周期内卫星轨道平面与地月连心线共面.求在该周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间(有M､m､R､R1､r､r1和T表示,忽略月球绕地球转动对遮挡时间的影响).
如图所示，相距
、质量均为M，两个完全相同木板A、B置于水平地面上，一质量为M、可视为质点的物块C置于木板A的左端。已知物块C与木板A、B之间的动摩擦因数均为
，木板A、B与水平地面之间的动摩擦因数为
，最大静摩擦力可以认为等于滑动摩擦力，开始时，三个物体均处于静止状态。现给物块C施加一个水平方向右的恒力F，且
，已知木板A、B碰撞后立即粘连在一起。
（1）通过计算说明A与B碰前A与C是一起向右做匀加速直线运动。
（2）求从物块C开始运动到木板A与B相碰所经历的时间
。
（3）已知木板A、B的长度均为
，请通过分析计算后判断：物块C最终会不会从木板上掉下来？
如图所示，在匀强磁场中有一倾斜的平行金属导轨。导轨间距为L，长为3d，导轨平面与水平面的夹角为
，在导轨的中部刷有一段长为d的薄绝缘涂层。匀强磁场的磁感应强度大小为B，方向与导轨平面垂直。质量为m的导体棒从导轨的顶端由静止释放，在滑上涂层之前已经做匀速运动，并一直匀速滑到导轨底端。导体棒始终与导轨垂直，且仅与涂层间有摩擦，接在两导轨间的电阻为R，其他部分的电阻均不计，重力加速度为g。求：
（1）导体棒与涂层间的动摩擦因数
；
（2）导体棒匀速运动的速度大小v；
（3）整个运动过程中，电阻产生的焦耳热Q。
如图所示，足够长、宽度L1＝0.1m、方向向左的有界匀强电场场强E＝70 V/m，电场左边是足够长、宽度L2＝0.2 m、磁感应强度B＝2×10－3 T的有界匀强磁场。一带电粒子电荷量q=＋3.2×10-19C，质量m＝6.4×10－27 kg，以v＝4×104 m/s的速度沿OO′垂直射入磁场，在磁场中偏转后进入右侧的电场，最后从电场右边界射出。（粒子重力不计）求：
（1）带电粒子在磁场中运动的轨道半径和时间；
（2）带电粒子飞出电场时的速度大小。
半径R = 40cm竖直放置的光滑圆轨道与水平直轨道相连接（如图所示）。质量m = 50g的小球A以一定的初速度由直轨道向左运动，并沿圆轨道的内壁冲上去。如果A经过N点时的速度v1= 6m/s，A经过轨道最高点M后作平抛运动，平抛的水平距离为1.6m。求：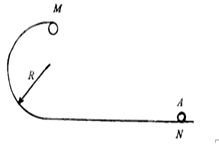
（1）小球经过M时速度多大；
（2）小球经过M时对轨道的压力多大；
（3）小球从N点滑到轨道最高点M的过程中克服摩擦力做的功是多少。（g=10m/s2）
如图所示，一水平传送带始终保持着大小为v0＝4m/s的速度做匀速运动。在传送带右侧有一半圆弧形的竖直放置的光滑圆弧轨道，其半径为R=0.2m，半圆弧形轨道最低点与传送带右端B衔接并相切，一小物块无初速地放到皮带左端A处，经传送带和竖直圆弧轨道至最高点C。已知当A、B之间距离为s=1m时，物块恰好能通过半圆轨道的最高点C，（g=10m/s2）则：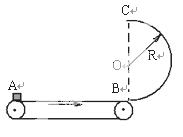
(1) 物块至最高点C的速度v为多少?
(2) 物块与皮带间的动摩擦因数为多少？
(3) 若只改变传送带的长度，使滑块滑至圆弧轨道的最高点C 时对轨道的压力最大，传送带的长度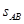
应满足什么条件？