某校数学课题小组了解到：6个牛奶盒经过工艺处理可以制作成一个卷纸。为了解市民节约和环保意识，该课题小组调查了本市100户经常饮用牛奶的家庭对牛奶的处理方式，并制成如下统计图。
（1）这100户家庭中有多少户扔掉牛奶盒？
（2）如果该市有1万户经常饮用牛奶的家庭，请估算扔掉牛奶盒的家庭有多少户？
（3）若（2）中这1万户家庭每户一年平均饮用90盒牛奶，请估算一年扔掉的牛奶盒可以制作成成多少个卷纸？
先化简，再求值：
3x
y－［5xy－（4xy－3）+2xy］,其
中x=－3，y=2
计算：
如图3，已知点
、点
分别在
的边上，请根据下列语句画出图形：
（1）作的余角
；
（2）作射线
与
相交于点
；
（3）取
的中点
，连接
.
如图，在平面直角坐标系xOy中, 正方形OABC的边长为2cm, 点A、C分别在y轴的负半轴和x轴的正半轴上, 抛物线y=a
+bx+c经过点A、B,最低点为M，且
＝
(1)求此抛物线的解析式.，并说明这条抛物线是由抛物线y=a怎样平移得到的。
(2)如果点P由点A开始沿着射线AB以2cm/s的速度移动, 同时点Q由点B开始沿BC边以1cm/s的速度向点C移动，当其中一点到达终点时运动结束.
①在运动过程中，P、Q两点间的距离是否存在最小值，如果存在，请求出它的最小值。
②当PQ取得最小值时, 在抛物线上是否存在点R, 使得以P、B、Q、R为顶点的四边形是梯形? 如果存在, 求出R点的坐标, 如果不存在, 请说明理由.
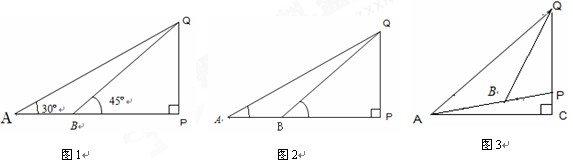
如图（1），在地面A、B两处测得地面上标杆PQ的仰角分别为30°、45°, 且测得AB=3米,求标杆PQ的长
(2)在数学学习中要注意基本模型的应用，如图(2),是测量不可达物体高度的基本模型：在地面A、B两处测得地面上标杆PQ的仰角分别为
，且测得AB=a米。
设PQ=h米，由PA-PB=a可得关于h的方程，解得h=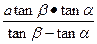
（3）请用上述基本模型解决下列问题：如图3，斜坡AP的倾斜角为15°，在A处测得Q的仰角为45°，要测量斜坡上标杆PQ的高度，沿着斜坡向上走10米到达B，在B处测得Q的仰角为60°，求标杆PQ的高。（结果可含三角函数）