袋中装有m个红球和n个白球，m≥n≥2，这些红球和白球除了颜色不同以外，其余都相同．从袋中同时取出2个球．
（1）若取出是2个红球的概率等于取出的是一红一白的2个球的概率的整数倍，试证：m 必为奇数；
（2）若取出的球是同色的概率等于不同色的概率，试求m+n≤40的所有数组(m，n)．
已知等差数列
满足：
，
，的前n项和为
．
(Ⅰ) 求
及；
(Ⅱ) 令
(
)，求数列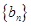
的前n项和
．
设集合A为函数y＝ln(－x2－2x＋8)的定义域，集合B为函数y＝x＋
的值域，集合C为不等式(ax－
)(x＋4)≤0的解集．
(1)求A∩B；
(2)若C⊆∁RA，求a的取值范围．
已知函数
的定义域为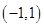
，且同时满足下列条件：
（1）是奇函数；
（2）在定义域上单调递减；
（3）
求
的取值范围。
已知集合A=｛x|x2-3x-10≤0｝,B=｛x|m+1≤x≤2m-1｝,若A∪B=A，求出实数m的取值范围。
已知p：方程x2＋mx＋1＝0有两个不相等的负根；q：方程4x2＋4(m－2)x＋1＝0无实根．若p或q为真，p且q为假，求m的取值范围．