某市医疗保险实行定点医疗制度,按照“就近就医、方便管理”的原则,参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为本人就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在的地区附近有A,B,C三家社区医院,并且他们对社区医院的选择是相互独立的.
(I)求甲、乙两人都选择A社区医院的概率;
(II)求甲、乙两人不选择同一家社区医院的概率;
(III)设4名参加保险人员中选择A社区医院的人数为ξ,求ξ的分布列和数学期望.
(本小题满分12分)已知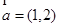 ,
, ,当
,当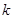 为何值时,
为何值时,
(1)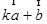 与
与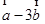 垂直?
垂直?
(2)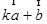 与
与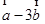 平行?平行时它们是同向还是反向?
平行?平行时它们是同向还是反向?
(本小题满分10分)已知指数函数 ,当
,当 时,有
时,有 ,解关于x的不等式
,解关于x的不等式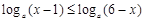
(本小题满分14分)已知圆 的圆心为原点
的圆心为原点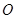 ,且与直线
,且与直线 相切。
相切。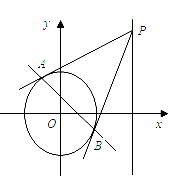
(1)求圆 的方程;
的方程;
(2)点 在直线
在直线 上,过
上,过 点引圆
点引圆 的两条切线
的两条切线 ,切点为
,切点为 ,求证:直线
,求证:直线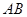 恒过定点。
恒过定点。
某工厂有214名工人, 现要生产1500件产品, 每件产品由3个A型零件与1个B型零件配套组成, 每个工人加工5个A型零件与3个B型零件所需时间相同. 现将全部工人分为两组, 分别加工一种零件, 同时开始加工. 设加工A型零件的工人有x人, 在单位时间内每人加工A型零件5k个(k∈N*), 加工完A型零件所需时间为g(x), 加工完B型零件所需时间为h (x).
(Ⅰ) 试比较 与
与 大小, 并写出完成总任务的时间
大小, 并写出完成总任务的时间 的表达式;
的表达式;
(Ⅱ) 怎样分组才能使完成任务所需时间最少?
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是CB、CD、CC1的中点,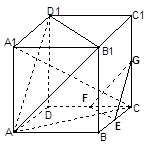
(1)求证:平面A B1D1∥平面EFG;
(2)求证:平面AA1C⊥面EFG.
(3)求异面直线AC与A1B所成的角