(本小题满分12分)
如图1,在平面内,ABCD边长为2的正方形,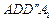 和
和 都是正方形。将两个正方形分别沿AD,CD折
都是正方形。将两个正方形分别沿AD,CD折 起,使
起,使 与
与 重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A
重合于点D1。设直线l过点B且垂直于正方形ABCD所在的平面,点E是直线l上的一个动点,且与点D1位于平面A BCD同侧,设
BCD同侧,设 (图2)。
(图2)。

(1)设二面角E – AC – D1的大小为q,当 时,求
时,求 的余弦值;
的余弦值;
(2)当 时在线段
时在线段 上是否存在点
上是否存在点 ,使平面
,使平面 平面
平面 ,若存在,求出
,若存在,求出 分
分 所成的比
所成的比 ;若不存在,请说明理由。
;若不存在,请说明理由。
(本题满分12分)
已知等差数列{an}的公差大于0,且 是方程
是方程 的两根,数列{
的两根,数列{ }的前n项和为
}的前n项和为 ,且
,且
(1)求数列{ }、{
}、{ }的通项公式;
}的通项公式;
(2)记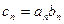 ,求证:
,求证:
(本小题满分12分)
某校选拔若干名学生组建数学奥林匹克集训队,要求选拔过程分前后两次进行,当第一次选拔合格后方可进入第二次选拔,两次选拔过程相互独立。根据甲、乙、丙三人现有的水平,第一次选拔,甲、乙、丙三人合格的概率依次为 ,
, ,
, 。第二次选拔,甲、乙、丙三人合格的概率依次为
。第二次选拔,甲、乙、丙三人合格的概率依次为 ,
, ,
, 。
。
(1)求第一次选拔后甲、乙两人中只有甲合格的概率;
(2)分别求出甲、乙、丙三人经过前后两次选拔后合格的概率;
(3)设甲、乙、丙经过前后两次选拔后恰有两人合格的的概率;
三.解答题:本大题共6个小题,共70分,解答应写出文字说明、证明过程或演算步骤.
17. (本题满分10分)
已知函数 ,
,
(1)求函数 的最小正周期;
的最小正周期;
(2)在 中,已知
中,已知 为锐角,
为锐角, ,
, ,求
,求 边的长.
边的长.
在直角梯形ABCD中, A为PD的中点,如下图,
A为PD的中点,如下图,
将△PAB沿AB折到△SAB的位置,使SB⊥BC,点E在SD上,

(1)求证:SA⊥平面ABCD;
(2)求二面角E-AC-D的 余弦值;
余弦值;
(3)在线段BC上是否存在点F,使SF//平面EAC?若存在,确定F点的位置,若 不存在,请说明理由?
不存在,请说明理由?