三．解答题：本大题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤.
17. (本题满分10分)
已知函数
，
（1）求函数
的最小正周期；
（2）在
中，已知
为锐角，
,
,求
边的长.
已知函数f(x)是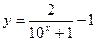
（x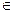
R）的反函数，函数g(x)的图象与函数
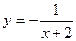的图象关于直线x=－2成轴对称图形，设F(x)=f(x)+g(x).
（1）求函数F(x)的解析式及定义域；
（2）试问在函数F(x)的图象上是否存在两个不同的点A,B，使直线AB恰好与y轴垂直？若存在，求出A,B坐标；若不存在，说明理由.
某商品在近30天内每件的销售价格p（元）与时间t（天）的函数关系是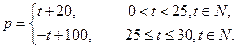
该商品的日销售量Q（件）与时间t（天）的函数关系是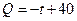
，求这种商品的日销售金额的最大值，并指出日销售金额最大的一天是30天中的第几天？
已知函数f(x)=lg(ax2+2x+1)
（1）若f(x)的定义域是R，求实数a的取值范围及f(x)的值域；
（2）若f(x)的值域是R，求实数a的取值范围及f(x)的定义域.
已知函数
(a、b是常数且a>0，a≠1)在区间[－
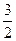，0]上有ymax=3，
ymin=
，试求a和b的值.
设函数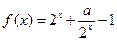
（a为实数）
（1）当a＝0时，若函数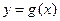
的图象与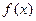
的图象关于直线x=1对称，求函数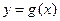的解析式；
（2）当a<0时，求关于x的方程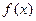＝0在实数集R上的解.